Projectile Motion

Projectile motion occurs when objects are fired at some initial velocity or dropped and move under the influence of gravity.
One of the most important things to remember about projectile motion is that the effect of gravity is independent on the horizontal motion of the object. The independence of the horizontal and vertical components of the motion of the object is often used in these type of physics problems.
It also accounts for the counterintuitive observation that a bullet fired horizontally from a gun takes the same time to fall to the ground as a bullet that is dropped from the same height.
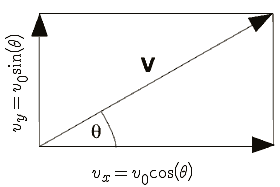
To be able to solve projectile problems you will often need to resolve the motion into its components.
$${v_x = v_0 \cos(\theta)}$$
$${v_y = v_0 \sin(\theta)}$$
Projectile Motion Flash Simulation
The Flash simulation can be used to try the concepts talked about below. Use the up and down arrow keys on your keyboard to raise and lower the cannon barrel. The left and right arrow keys alter the amount of power in the explosion. Press the fire button to fire (obviously). The path with air resistance can be switched on using the tick box and when you feel there are too many traces on the screen they can be cleared using the clear trace button.
Use the cannon to find the maximum height, maximum range for a particular velocity of cannon ball.
Compare the parabolic flight path of the cannonball with the path of the cannonball taking air resistance into account. How is it different?
For a projectile without air resistance, the angle that gives the maximum range is 45° try and find the angle for maximum distance. Does the angle change with velocity?
Balistics
Consider a cannonball fired from a cannon. The barrel of the cannon points at an angle θ from the horizontal. This is known as its elevation. When the cannon is fired the explosion and expansion of the gases created accelerate the cannonball until it leaves the barrel. The velocity with which it leaves the barrel is known as the muzzle velocity.
To understand the motion of the ball, the velocity can be resolved into horizontal and vertical components. Experiments, taking multiple images with strobe light of projectiles, show that the horizontal component of velocity is constant with time. That is, the object travels at the same horizontal speed throughout the motion.
The vertical component has gravity acting against the projectile so its motion is that of an object that has been thrown into the air or dropped from a platform.
When these two motions are combined, the resulting path is known as a parabola.

Even for extended complicated objects the motion is roughly parabolic. Divers diving into a swimming pool, motorcross riders. Although the motion of the object may be very complicated if you work out where the centre of mass is and follow this point, it will move in a parabolic trajectory.

Projectile motion problems can be solved using the equations of linear motion.
The horizontal motion is given by:
$${x(t) = v_x t}$$
While the vertical motion is:
$${y(t) = v_y t - \frac{1}{2} g t^2}$$
Often question about projectiles will ask you to find the maximum height, or the range of the projectile, or even how long it took for the projectile to hit the ground.
Maximum Height
When the projectile reaches its maximum height its vertical component of velocity will be zero. We can use the linear equations of motion to calculate this height, h.
From $v^2 = u^2 + 2 a s$ where $v$ is the final velocity, $u$ is the initial velocity, $a$ is the acceleration in this case provided by gravity and $s$ is the distance covered or in our case the height $h$.
The final velocity is zero. So, substituting our symbols we have
$${v_y^2 - 2 g h = 0}$$
But $v_y$ is $v_0 \sin(\theta)$
$${h=\frac{(v_0 \sin(\theta))^2}{2g}}$$
Time of Flight
We can use the independence of the horizontal and vertical motions of the projectile to determine the time of flight. If we know the initial velocity, we can work out the time. The vertical motion looks like that of a ball being thrown upward. At its highest point the velocity will be zero. We just need to find the time that it takes and multiply by two, since what goes up, must come down.
Recall from the linear equations of motion, $v = u + a t$
$${v_0 = 0 + a t}$$
So, rearranging, $v_y - g t = 0$
$v_0 \sin(\theta) - g t = 0$
Therefore, $${t =2\frac{v_0 sin(\theta)}{g}}$$
Range
Since the trajectory in the absense of air resistance is symmetrical about the point of maximum height, it will be half way through its motion so the range will be twice the distance it takes to travel in this time.
The horizontal distance is just,$s = ut$. Inserting the horizontal component of velocity $s = v_0 cos(\theta) t$
and using the argument in the previous section to calculate the time to reach the maximum height, not forgeting to multiply by 2, we obtain
$${s = 2v_0 cos(\theta) \frac{v_0 sin(\theta)}{g}}$$
The identity $2\sin(\theta)\cos(\theta) =\sin (2\theta)$ can be used to simplify the expresion further.
$s =\frac{v_0^2\sin (2\theta)}{g}$
If the projectile is fired at some height h_0 above the ground that it lands on we must find the additional time that it stays in the air.
$h = h_0 + v_y t - \frac{1}{2} g t^2$
To find the time involves solving this quadratic equation in $t$.
$${t =\frac{v_y\pm\sqrt{(v_y^2 + 2 h_0 g)}}{g}}$$
We are only interested in the positive solution since a negative value for time is not physical.
$${t =\frac{(v_0 \sin(\theta) + \sqrt{(v_0 \sin(\theta))^2 + 2 h_0 g}}{g}}$$
$${s = \frac{v_0\cos(\theta)[(v_0 \sin(\theta) + \sqrt{(v_0\sin(\theta))^2 + 2 h_0 g}]}{g}}$$
To check that this expression is correct, it should return to the expression for range on level ground when $h_0 = 0$.
Maximum Range with Angle
But what about the greatest range? For a projectile fired on level ground and neglecting air resistance, the range is determined from the equation $s =(v_0^2/g) \sin(2\theta)$
Looking at this expression can see it is a constant multiplied by a sine function. It will have a maximum when sine is 1. We know this happens when $\theta = 90^{\circ}$. So to get 90$^{\circ} \theta$ must be 45$^{\circ}$. The maximum range would be
$${s_{max} = v_0^2 / g}$$
If we didn't know this, we could differentiate the equation for range with respect to θ and set the result equal to zero.
$${\frac{d(v_0^2\sin(2\theta)/g)}{d\theta} = \frac{2v_0^2}{g}\cos(2\theta)}$$
If you plot this over a range from 0 to 90$^{\circ}$, it is zero at 45$^{\circ}$. So the angle that will give the greatest range is 45$^{\circ}$
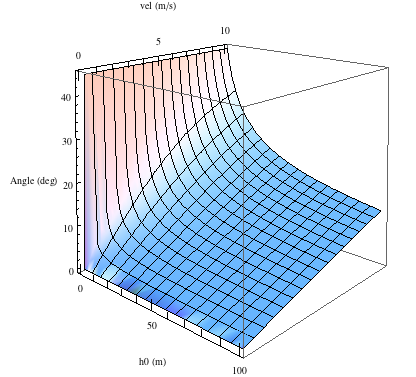
Maximum Range From a Height $h_0$
When the projectile is fired from a height $h_0$ above the landing ground the angle for maximum range is not 45 ° but it can be found in a similar way.
Take the equation for range from a height, and differentiate. A rather tedious exercise in calculus lead us to the following expression.
$${\frac { dR } { d\theta} = \frac {v^2} {g} [ \cos \theta ( \cos \theta + \frac {\sin \theta \cdot \cos \theta} {\sqrt {(\sin \theta)^2 + C} } ) - \sin \theta ( \sin \theta + \sqrt { ( \sin \theta )^2 + C })}$$
Where $C$, is $C = \frac {2 g h_0} { v^2}$
Substituting $u = (\cos \theta)^2$ and $1 - u = (\sin \theta)^2$ produces:
$${u + \frac {u \sqrt {1-u}} {\sqrt {1-u+C}} - (1-u) - (\sqrt {1-u}) \sqrt {1-u+C} = 0}$$
This can be reduced to
$u = \frac {C + 1} {C + 2}$
$\theta = \arccos \sqrt { \frac {2 g h_0 + v^2} {2 g h_0 + 2 v^2} }$
Effect of air Resistance
In the real world, air resistance has a marked effect on the motion of a projectile. If the object is light, then it does not have the inertia to push through the air. Air resistance, often called drag creates an additional force on the projectile that acts in the opposite direction to the velocity.
For objects that move through air and at high velocity, the air resistance is proportional to the square of the velocity.
$D = \frac{1}{2}CA\rho v^2$
To calculate the path of the projectile with air resistance, we need to know the forces acting on the projectile. We know that gravity will always act vertically downward on the projectile. The air resistance creates a force, that is always in the opposite direction to the velocity.
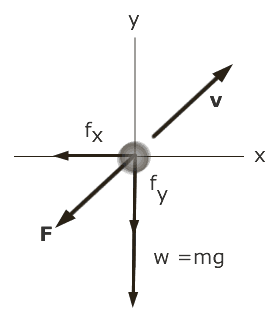
From Newton's second law, $F = m a$, we can see that this force will have its effect by changing the acceleration of the cannon ball. In the x direction it will act to decelerate the projectile reducing its range. It will also act on the vertical component of velocity slowing the projectile on both the upward and downward part of the motion.
The motion is described by summing the forces in the x and y directions. In the x-direction,
$${\sum{F_x} = - F_{drag_x}}$$
$${\sum{F_y} = - F_{drag_y} - m g}$$
To find the path of the projectile we must solve two differential equations.
Since acceleration is the second derivative of the position we can write a differential equation which the motion.
$${\frac{d^2x(t)}{dt^2} = - \frac{D}{m} \frac{dx(t)}{dt} = 0}$$
$${\frac{d^2y(t)}{dt^2} = - \frac{D}{m} \frac{dy(t)}{dt} - g}$$
$${v=\sqrt{v_x^2 + v_y^2}}$$
These are non-linear and so cannot be solved analytically. Numerical solution is possible however. To solve numerically, we make the assumption that the over a small enough interval of time we can come approximate the solution by applying the linear equations of motion, to obtain velocities and then the position of the projectile.
Before we do that however we should rewrite the differential equations. We know that the drag is proportional $v^2$. But $v$ is a vector so, $v^2 = v \vec v = v v_x$ and $v v_y$
The constant term in is made up of several factors such as the density of air, cross-sectional area, drag coefficient, but none of these vary with time for our purposes, so we are okay to bundle them up as a number. Let's call it $k$, it is actually, $k = \frac{CA\rho}{2 m}$
$a_x = - k v v_x$
$a_y = - k v v_y - g$
We can compute the new velocities in the $x$ and $y$ directions after a short time $dt$. The new velocities will be.
$v_{x_{new}} = v_x + a_x dt$
$v_{y_{new}} = v_y + a_y dt$
Once we have the new velocities we can calculate the new position of the cannonball
$x_{new} = x + v_x dt + a_x dt^2$
$y_{new} = y + v_y dt + a_y dt^2$
