Damped Oscillations
In real life, the oscillations lose energy which reduces the total mechanical energy of the system.The amplitude of the oscillations can be reduced more rapidily if a damper is added to the system. Dampers disipate the energy of the system and convert the kinetic energy into heat. A common form of damper design will consist of a piston that moves in a viscous liquid.
Modelling Damping
Damping creates a force which acts in the opposite direction to the object travel. For object moving slowly in liquids the damping force is proportional to the velocity. Therefore we can write:
Fdamping = - 2 b v = - 2 b x'(t)
The factor of two serves to simplify the expression later. It has no physical significance. We can now add the new force term to the simple harmonic motion differential equation and we simplify things later we choose γ = b/(2m) and &omega2 = k/m
m x''(t) + γ x'(t) + &omega2x(t) = 0
We can solve this equation by substituting a trial solution of the form
x(t) = A exp(λt)
Inserting this into the differential equation
λ2 A exp(λt) + 2γ λ A exp(λt) - ω2 A exp(γt) = 0
or
λ2 + 2γλ - ω2 = 0
This is a quadratic equation with two solutions of
λ = [ -γ ± (4γ2 - 4&omega2)1/2]/2
λ = -γ ± (γ2 - ω2)1/2
It is the term -γ ± (γ2 - ω2)1/2 that leads to the interesting behaviour of the system.
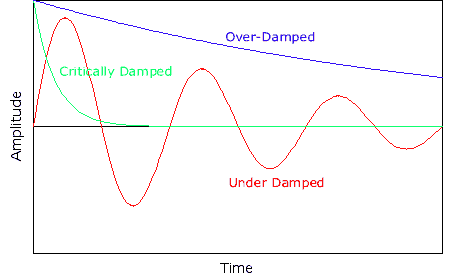
Over Damping
When γ2 > ω2 this leads to real values for the value of lambda. Therefore the solution will be
y(t) = C1 exp[(-γ ± (γ2 - ω2)1/2)t + C2 exp[(-γ ± (γ2 - ω2)1/2)t)]
y(t) = e-γt[C1 e(γ2-ω2)1/2 +C2 e(γ2 - ω2)1/2]
Depending on the inital conditions, the mass has so much dampling that it takes a long time to reach its equilibrium position.
Critical Damping
Here γ2 = ω2, the damping is such that the system returns to the equilibrium without overshooting the equilibrium position. The system reaches equilibrium in the shortest time without overshooting. An example of a critically damped system is a car's suspension. In this application we would not like the car to oscillate each time it went over a bump. The motion could lead to a loss of control of the car and at the very least would lead to a uncomfortable ride possibily leading to car sickness.
The solution becomes:
exp(-γt) [A exp((γ2 - ω2)1/2t) + Bt exp((γ2 - ω2)2t)]
Light Damping
(γ2 - ω2) < 0. This results in a negative value for this term, and leads to a complex number for λ
Therefore, the total solution is a decaying exponential solution multiplied by a cosine function.
y(t) = exp(-γ)[A cos(&lambdat) + B sin(λt)]
y(t) = Cexp(-&gammat) cos(λ - φ) where &lambda = (ω2 - γ2)1/2
Once again, C = (x02 + (v0/ω)2)1/2 and &phi = tan-1(v0/x0ω)
Period of Decay
How does the damping affect the period of the oscillation. The time between sucessive oscillations is given by
T = 2π/λ = 2π/(ω2 - γ2)1/2
Clearly this only makes sense when γ2 > &omega2, otherwise the result is complex. For larger values of the damping the period increases.
