Forced/Driven Oscillations
So far we have considered oscillations with damping such that the amplitude decays with time. What happens if in addition to the damping, we add energy into the system to keep it oscillation going. The driving force will be a cosine wave which acts on the system periodically.
The driving force has its own driving frequency which we shall call ω0 and it has an amplitude F. We can write the driving force as
Fforcing = F0 cos (ω0)
We can write the differential equation as
m x''(t) = - 2 γ - ω2 + F cos ωt
x''(t) + 2 γ + ω2 = f cos ωt
How do we solve this equation? It look very similar to the equation for damped harmonic motion if it didn't have the driving force term on the end.
The general solution to this equation is given by the characteristic solution plus a particular solution. We have already found the characteristic solution when we considered damped oscillations so it remains to find a particular solution.
Consider a solution of the form:
x(t) = c1 cos αt + sin αt
Differentiating once
-c1α sin αt + α cos αt
Differentiating again
-c1 α2 cos αt - α2 sin αt
Inserting equations (2) and (3) into (1) and factoring into terms involving cosines and sines gives:
-c1&alpha2 + 2c2γ + c1ω2) cos αt = F0 cos αt
(- c2α2 - 2c1γ α + c2ω2) sin αt = 0
All objects can oscillate if the conditions are right. It will have a frequency at which it will vibrate if energy is given to it. This is called the nautral frequency. It is important in many engineering disiplines to ensure that the natural frequency of vibration is not driven by external factors. Bridges are a good example of this. The Tacoma Narrows bridge in Washington oscillated wildly because its natural frequency was very close to that caused by the wind. Eventually, this lead to the bridge falling into the river. The millenium bridge also suffered from vibration caused by the natural frequency of the people walking across it. Such oscillations were fixed by adding damping.
To keep the system oscillating, energy must be supplied. Otherwise the system will oscillate and the amplitude of the oscillations will decrease as energy is lost. The system can be given energy by supplying energy periodically to the system much in the same way that a parent would keeps a child on a swing swinging by pushing the swing. As the swing comes back and reaches its maximum displacement, a push emparts energy to keep it going.The frequency with which we supply energy is known as the driving frequency.
We can investigate the effect of the driving frequency on the oscillation of a spring mass system. A motor supplies a driving force to the spring which causes the mass to oscillate on the spring. If the driving frequency is much less than the driving frequency the amplitude of the oscillations of the spring mass system are small.
Similarly, if the driving frequency is much greater than the natural frequency, the inertia of the mass prevents the mass from reacting quickly enough and the oscillations have a small amplitude.
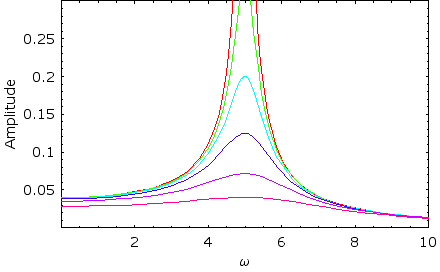
If the driving frequency is close to the natural frequency then energy is transferred to the system with very little resistance. This causes the amplitude of the resulting oscillations to become very exagerated and much larger than the amplitude of the driving force. This phenomena is known as resonance
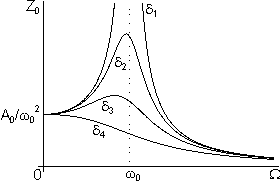
With increased damping, the peak of resonance decreases
Looking at the phase difference between the driving oscillation and the mass, we can see that resonance occurs when the phases is π/2. This is what resonance really is, it is the efficient transfer of energy from the driving system to the pasive system.
Examples of Resonance
Many types of object resonate as a result of being driven by the wind. Furthermore, the oscillations can occur in many different ways, called oscillating modes.These oscillations are potentially dangerous and to limit their effect, helical strakes are placed on the top of chimneys.
Resonance is an important part in the design of musical instruments. Pianos acoustic guitars, violins use resonance to amplify and shape the sound produced. An interesting article on the Violin acoustics: an introduction
