Work

We often use words in physics that have a different a meaning from their everyday useage. Work is a good example of this. The scientific definition is

Work, is the product of the resolved force F, acting in the direction of motion, and the displacement through which the object travels.

If the force, F does not cause the object to move, then no work is done. A man holding a heavy weight in the air is not doing any work in the scientific scense of the word, although it might be hard work to keep it in the air, which is converting chemical energy of the muscles into thermal energy by muscular action. Mathematically speaking,

Where F is the applied force, s is the displacement and θ is the angle between the force acting on the object and the direction of motion. Work is a scalar because of the dot product between two vectors.

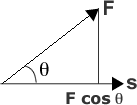
If the force acts in the same direction as the motion, then θ is 0 degrees then the work becomes, W=|F||s|, since cos (0)=1. Conversely, if the force is at right-angles to the displacement then θ= 90° and sin (90)=0;. Therefore force has no component in the direction of the displacement. i.e. the forces are independent. Therefore, the work done by the force is zero.

All this assumes the force acting on the object is constant with time. If the force varies with the distance then the work done could be found by plotting a graph of the force in the direction of motion against the displacement. For a small enough displacement the work done can be approximated by δW=F(s)δs.

The total work is then simply the sum of all the strips. As δ goes to zero then the sum becomes the integral. Therefore a new definition of work is

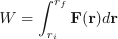
When the environment does work on a system, W > 0; that is, the total energy of the system increases. Work is done on the system.

When a system does work on its environment, W < 0; that is, the total energy of the system decreases. Work is done by the system.

Work is done by the system when the resolved force has a component in the same direction as the displacement. If the resolved force has a component in the opposite direction to the displacement, the work done is negative since cos θ <1 for θ > 90 °. For example when two surfaces slide over each other the work done by the frictional forces is always negative, since the frictional force opposes the relative motion.

For a variable force, the work done can be found by plotting the component of force in the direction of the displacement, as a function of the displacement. The work done is the area under the curve.

The unit of work is the [N.m]. This derived unit is named after John Prescot Joule who did much work on the conversion of energy from one form of to another. A Joule is defined as:

One Joule is the work done by a force of 1 Newton when its point of application moves through a distance of 1 metre in the direction of the force. 1 [J]= 1 [N.m]

Conservative Fields

If an object is moved around a closed path and returns to its original position. How much work is done on the object? The answer depends on whether the system is conservative or non-conservative.

Examples of conservative field are gravitational potential field as long as friction is neglected.