Gravitation

The Gravitational Field

Figure 1. A Uniform field

Figure 2. Gravitational
field on a larger scale.

Figure 3. The Earth's gravitational
field as a whole.

We can represent the force of gravitational attraction as a field. A field is a graphical representation of the strength of a force and the direction in which the force is felt.

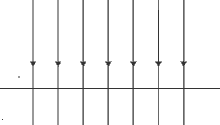
In a local region on the surface of the Earth the gravitational field is essentially uniform. We can see this because the number of field lines per unit are does not change. If the force was stronger in a particular region, the number of field lines in that region would increase. The lines of force act downwards toward the centre of the Earth but on this scale the gravitational field is uniform as shown in Figure 1.

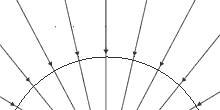
On a larger scale, the gravitational field varies in direction and magnitude. The direction of the field lines is perpendicular to the surface of the Earth. As the height above the surface of the Earth increases the magnitude of the force decreases as is shown by the increasing separation of the field lines.

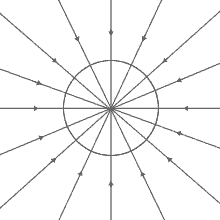
Considering the Earth as whole, (Figure 3), the gravitational field is directed toward the centre of the Earth. On opposite sides of the Earth the gravitational field has an opposite magnitude.

Universal Law of Gravitation

The Earth exerts a gravitational force on a person and a the person exerts the same but opposite force on the Earth. Issac Newton was the first person to understand that it was gravity that was responsible for apples falling to the ground but it is also the same force that keeps the Moon in orbit around the Earth.

force is proportional to mass and inversely proportional to the square of the distance

Figure 4. Force is proportional
to mass and inversely proportional to
the square of distance

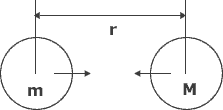
The force of gravity always acts between pairs of bodies and is proportional to their masses. However, the force of gravity also depends on the distance between the two bodies. As the two bodies are moved further apart, the gravitational force between them decreases with the square of their distance apart.

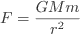$F=-\frac{GMm}{r^{2}}$ (1)

where m and M are the masses of the two bodies, respectively and r is the distance between the two bodies centres of mass. The constant of proportionality is called the universal constant of gravitation or also 'big-G' and has a value of 6.67 x 10^-11 N.m².kg^-2 or m^3.kg^-1.s^-2

Flash animation. The force of gravity on a 1-kg mass.

Acceleration due to Gravity

We measure are familiar with measuring the weight of an object as the force attracting it to the centre of the Earth using F=mg. Combining this equation with the equation for the universal law of gravitation we obtain, g= GM/r². Thus the force of gravity depends on the mass of the body and is inversely proportional to the square of the distance r.

Weightlessness

When an astronaut is floating in space, they feel as if they have no weight, yet as we have seen the force of gravity extends far beyond the atmosphere. It decreases with the square of the distance, but there is a gravitational force acting on every object. Weightlessness is caused because the spacecraft and everything inside is travelling in orbit and so everything is effectively falling at the same rate.

Variation of g with Distance

The Earth's gravitational acceleration decreases with height above the surface with an inverse square relationship. At the Earth's surface g=GM_E/R_E. At a distance of twice the Earth's radius from the Earth's centre, 2 r_E the gravitational acceleration is GM_E/4. At 3 r_E, g=GM_E/9 and so on.

r	g
1 r_E	GM/r_E²
2 r_E	GM/4r_E²
3 r_E	GM/9r_E²
4 r_E	GM/16r_E²
5 r_E	GM/25r_E²

The plot shows this variation as a function of distance from the centre of the Earth

Figure 5. Variation of g with distance measured in terms of Earth radii. The green line shows more accurate theoretical values.

Figure 6. Calculating g inside the Earth

What is the value of g inside the Earth? If we assume that the Earth has a constant density, we can work out the mass from the equation

mass= density x volume

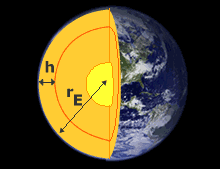
Assuming also that the Earth is spherical, (it is actual an oblate spheroid, that is to say, wider at the equator than at the poles). The volume of a sphere is V = 4/3 π r_E³. Where r_E is the radius of the Earth (6400 km).

If we were to dig down into the Earth a distance h, the new radius would be r_E-h. The mass that produces a gravitational force is (4/3) π (r_E-h)³ ρ

Then the value of gravitional acceleration inside the Earth is

g= (4/3) G π (r_E-h)³ ρ/(r_E-h)²= (4/3) G ρ π (r_E-h)

This has a linear or straight-line dependence on the radius. The density can be found by calculating the mass and volume of the Earth. ρ=M_E/V_E.

A more advanced theoretical prediction of the magnitude of gravity is shown by the green line in Figure 6. The real variation in gravity depends on the variation of density of the material with depth.

Mapping the variation in g

The variation in the Earth's gravitational field is measured continuously and accurately by the Gravitational Recovery And Climate Experiment (GRACE) satellites. These satellites follow each other in identical orbits but separated a short distance apart.

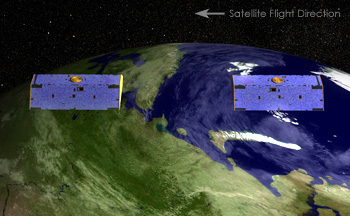
(GRACE) satellites measuring the variation in the gravitational field of the Earth.

If the Earth had a constant density, then the distance between the satellite would not change as they orbited the Earth. However, slight variations in the gravitational field cause the satellites to come closer together or drift away from each other.

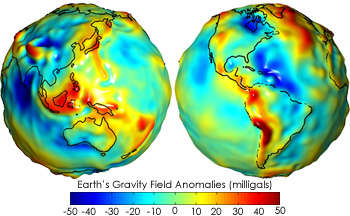
Earth's gravitational field anomalies (milligals).

The variation in the Earth's gravitational acceleration is shown in the figure. The variation in gravity is 9.80665 ms² ± 50 milligals (The galileo is the cgs unit of acceleration, 1 gal = 0.01 m/s²).

Gravitational Force and the Moon

Newton was the first to consider that the force responsible for pullling objects to the ground (such as apples) might also be responsible for keeping the moon in its circular orbit. He knew that the gravitational force decreased with height above the Earth's surface but he did not know how it varied. The distance of the Earth to the Moon was well established, as was the time taken for the moon to orbit the Earth. From this information, Newton was able to calculate the gravitation acceleration responsible for the centripetal force. With T as 27.3 days, r as 384,000 km or about 60 Earth radii. The acceleration a=v²/r = (2πr/T)²/r this is 0.00272 ms². The acceleration due to gravity on Earth, g_E is 9.81 ms^-2. The ratio of g_E/g_m≈3600, meaning that the gravitational force of attraction keeping the moon in orbit is 3600 times less than on Earth. At a distance of 60 r, 3600 times less gravity would be the same as if the gravitational force had an inverse square dependence. (ie. 60 r². Newton had discovered how the law of gravity decreases with distance just by knowing the time it takes the moon to orbit the Earth, its distance from the Earth and the value of gravity on the Earth. Which is yet another reason why he is regarded as one of the foremost scientists in history.

Gravitational Force and the Motion of the Planets

While it was convincing that the moon travelled around the Earth under the influence of gravity. It did not necessarily mean that the planets were also kept in their orbit by the gravitational force. Kepler had discovered three laws concerning the motion of the planets. His third laws states that the square of the period of motion over the cube of the distance is a constant. Assuming that the planets orbit the Sun in a circular orbit then the centripetal acceleration is a=v²/r_m, where v is the velocity of the moon around the Earth. The velocity, is given by the distance/time where the distance is the circumference, 2πr of the orbit and T is the period of the moon's orbit. Therefore, the velocity is (4π²/r²)

The centripetal acceleration is provided by the acceleration due to gravity. It has a magnitude, g=GM₀/r².

a=v²/r=(4πr_m²/T²)/r

Therefore, GM₀/r²=4πr_m/T_m²

T²/r_m³=4π²GM₀

Since the mass and the universal constant of gravity do not change, Newton had shown that the force of gravity was responsible for keeping the planets in their orbits.

Gravitational Potential

The definition of the gravitational potential field is

The potential is defined as the work done in bringing a body of unit mass from infinity to a point. Since work is done by gravity on the body the work done is negative.

In mathematical terms,

$V=\int F(r){dr}=\int\frac{GMm}{r^{2}}dr=\left[-\frac{GMm}{r}+c\right]=-\frac{GMm}{r}$

The zero for gravitational potential is taken at infinity because it is a convenient reference point for any object in the universe. Remember that for the zero of gravitational potential energy, we choose the Earth as a convenient reference point. There is no inconsistancy with this as only differences in potential are significant.

Gravitational potential is always negative indicating that the field does work in moving an object closer. The figure below shows the gravitational potential for the Earth and moon. The potential fields add together algebraically. We can see that to send a rocket to the moon we need only provide the force for the rocket to escape the Earths gravitational potential field and enter the moon's gravitational potential field. After this the rocket will accelerate towards the moon by the pull of the moon's potential.

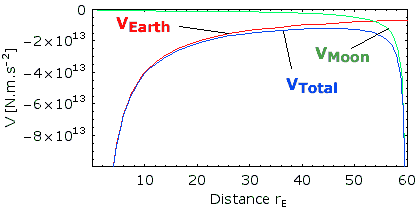
The gravitational potentential of the Earth, Moon and their sum.

The force on an object at a given potential is given by the slope of the potential at that point.

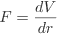
$F=\frac{dV}{dr}$

Escape Velocity

If the kinetic energy given to an object is equal to the gravitational potential then neglecting air resistance, the object could escape from the Earth's gravitational field.

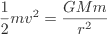
$\frac{1}{2}mv^{2}=-\frac{GMm}{r}$

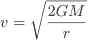
$v^{2}=2\frac{GM}{r}$

Notice that the escape velocity does not depend on the mass of the object but does depend on the mass of the body, M one is trying to escape from.

So, if we want a rocket to escape from the Earth's gravitaional field, how fast should it be travelling before the engines stop accelerating it?

Our formula states, v= √(2GM/r)

v = √(2 x 6.67 x 10^-11 [N.m².kg^-2] x 5.976 x 10²⁴ [kg]/6.378 x 10⁶ [m]

v = 11.17 x 10⁶ [m.s^-1] ≈ 11.2 km.s^-1

Body	Mass x M_E	Radius x r_E
Mercury	0.0558	0.398
Venus	0.815	0.95
Earth	1	1
The Moon	0.0123	0.273
Mars	0.107	0.532
Jupiter	318	11.2
Saturn	95.1	9.41
Uranus	14.5	4.06
Neptune	17.2	3.88

Table 2. Masses and radii of the planets in our Solar System. The International Astronomical Union (IAU) has ruled that Pluto is no longer to be classified as a planet but as a dwarf planet, therefore it has been omited from the list. However, its mass and radius are (0.01 m_E and 0.2 r_E), respectively. Also shown is the data for the Moon.

Gravitational Potential Energy

Remember the definition for gravitational potential energy, P.E.=m g h an now we are saying the gravitational potential is V=-GMm/r. Isn't there some inconsistancy? It can be shown that on differences in potential energy are important.

Let r=r_E+h, where h<<r_E. Then V(r)-V(r_E) =GMm(1/r_E-1/r) is the difference in gravitational potential.

GMm(r_E+h-r_E)/(r_E(r_E+h)

≈GMm(h/r_E²)

=mgh since g=GM/r²

Summary

Fields are a graphical illustration of the forces exerted on a unit mass in space. Field strength is shown by the number of field lines per unit area. Gravitational fields are alway attractive.

The force between two bodies of mass M and m is F=GMm/r² where M and m are the masses of two bodies, r is the distance between them. Where G is the universal constant of gravitation G=6.67 x 10^-11 [N.m²kg^-2] or [kg]

Site Search