Circular Motion
A body that travels an equal distances in equal amounts of time along a circular path has a constant speed but not constant velocity. This is because velocity is a vector and thus it has magnitude as well as direction
The velocity of P is directed along the tangent at P. The speed remains constant but the velocity has changed. We know that if the velocity changes with time then the ball on the string is also accelerating.
The Radian
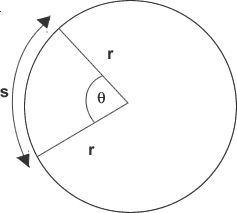
angles can be measured in radians as well as degrees. The angle in radians is defined by. If s = r then θ=1 rad. Therefore, 1 rad is the angle subtend at the center of a circle by an arc equal in length to the radius. When s =2π r then θ=2 π radians=360°. Therefore, 1 rad = 360°/2 π=57.3°
Since we are often dealing with angles and trigonomic functions, a useful approximation that is often used is that for small angles of &theta, sin θ and tan θ = θ where θ is measured in radians.
&theta = sin &theta = tan θ for small angles where theta is measured in radians.
Angular Velocity
The speed of a body moving in a circle can be specified either by its speed along the tangent at any instant (linear speed) or by the angular velocity. This is the angle swept out in unit time by the radius joining the body to the centre. It is measured in [rad s-1]
Further, the angular velocity is the time for the particle to travel around once divided by the period. ω = 2 π/T
Derivation
Consider a body moving uniformly from A to B in time t so that OA rotates through a small angle θ.
The angular velocity, ω of the body about O is ω=θ/t.
If arc AB has length s and v is the constant speed of the body, v=s/t
But s=r θ.
So, v=r θ/t and ω =θ/t,
therefore v=rω
Acceleration
The expression for the acceleration of an object moving in circular motion of radius r moving at a constant speedv is derived as follows. If it travels from A to B in a short interval of time δt then, since speed = distance x time, arc AB = vδt.
Also by the definition of angle in radians, arc AB = r δθ=v δt.
So, v δt/r = δθ.
The vectors vA and vB represent the velocities at these points. The change in velocity between A and B obtained by subracting vA from vB.
Change in velocity = vA and vB. Parallagram rule or triangle rule. The resultant is effectively XZ. Since one vector (-vA) is perpendicular to OA and the other vB is perpendicular to OA and the other vB is perpendicular to OB, therefore ∠ XYZ = ∠ AOB =δθ
If δt is small, the δθ is also small. Then the length of XZ in the figure will be almost the same as X'Y' in b) X'Z'=rδθ but also δθ=vδt/r. Therefore, X'Z'=v2/r δt.
a=change in velocity/time interval = (v2δt/r)/δt=v2/r. Therefore a=v2/r also a=ω2r.
The direction of the acceleration is toward the centre O as can be seen if δt is made so that A and B all but coincide; XZ is then perpendicular to vA (or vB) is along AO or BO. We say the body has a centripetal acceleration (i.e. centre seeking). Does a body moving uniformly in a circle have constant acceleration?
Centripetal Force
Since a body moving in a circle (or circular arc) is accelerating, it follows that from Newton's 2nd law that there must be a force acting on it to cause the acceleration. This force will also be directed toward the centre and is called the centripetal force. It causes the body to deviate from the straight line motion it would naturally follow. The magnitude of the centripetal force is given by:
Where m is the mass of the body and v is the speed in the circular path of radius r. If the angular velocity of the body is ω we can also say since v=rω.
Other examples of circular motion will be discussed in the following sections. In all cases it is important to appreciate that the forces acting on the body must provide a resultant force of magnitude mv2/r toward the centre.
Experimental Measurement of Centripetal Force
The turntable is rotated by the electric motor causing the truck of known mass m to move out from the centre of the turntable. Opposing the motion of the truck is a spring which provides the centripetal force required to keep the truck in position. As the speed of the turntable is increased the spring extends until the truck reaches the stop at the end of the rails. When the truck just hits the truck the extension of the spring is of known length. The velocity of the turntable can be found by measuring the time it takes for the turntable make ten revolutions and dividing by ten. The velocity it then 2π/t. We know the m and the radius and therefore the extension of the spring. We can also measure the force required to produce the same extension of the same using a spring balance and compare the two forces.
Rounding A Bend
If a car is travelling round a circular bend with uniform speed on a horizontal road, the resultant force acting on it must be directed to the centre. ie. it must be the centripetal force. This force arise from the interaction of the car with the air and the road. The direction of the force exerted by the air will more or less oppose the instantaneous direction of motion. The other more important horizontal force is the frictional force exerted inwards by the road on the tyres of the car. The resultant of these two forces is the centripetal force. If the centripetal force is less than the force wanting to pull the car out, a skid will result. Safe cornering that does not rely on friction is achieved by banking the road. The problem is to find the angle θ at which the bend should be banked so the centripetal force acting on the car arises entirely from a component of the normal force, N of the road.
Treating the car as a particle and resolving N vertically and horizontally we have, since N sinθ is the centripetal force. N sinθ=mv2/r where m and v are the mass, speed and r is the radius of the bend respectively. Also the car is assumed to remain in the same horizontal plane therefore no horizontal acceleration therefore, N cosθ=mg. Dividing both equations, tan θ=v2/rg
A bend in a railway track is also banked. In this case, so that at a certain speed no lateral thrust has to be exerted by the outer rail on the flanges of the wheels of the train, otherwise the rails are strained. The horizontal component of the normal forces of the rails on the train provide the centripetal force.
Aircraft
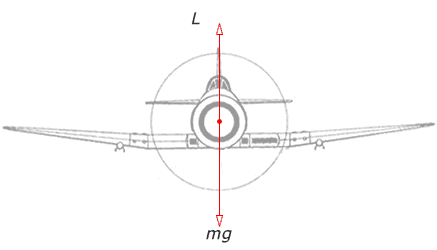
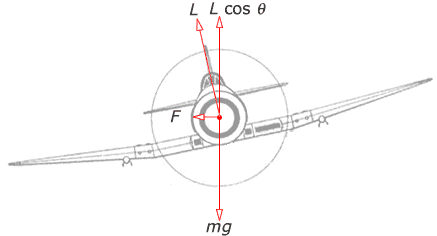
An aircraft in straight, level flight experiences a lift force perpendicular to the surface of its wings which balances its weight, mg. To make a turn, the ailerons are operated so that the aircraft banks and the horizontal component of the lift supplies the necessary centripetal force to make the aircraft turn. The lift force is always perpendicular to the wings and so the aircraft's weight has to be supported by the vertical component of the lift. Since this is slightly less than the weight of the aircraft, the aircraft will lose altitude unless the lift is increased by increasing the speed or pulling the nose of the aircraft up.
The Rotor
The rotor is often seen at a fairground. A cylinder of around 4 meters in diameter is set spinning. The passengers stand inside the cylinder against the wall as it spins. The rotational motion causes the passengers to be pinned to the wall of the rotor. When the rotor is spinning fast enough, the floor of the cylinder drops down and the passengers remain pinned to the walls. The forces acting on a passenger of m are shown. N is the normal force and is the centripetal force needed to keep him moving in a circle. Hence if r is the radius of the rotor and v the speed of the passengers then N=mv2/r. If F is the frictional force acting upwards between the passenger and the rotor wall and since there is no vertical motion of the passenger. F=mg. If μ is the coefficient of limiting friction between the passenger and the wall we have F=μN. Therefore, μN=mg, μ=mg/N=gr/v2. Note that this is independent of the mass m.
A typical value of μ between clothing and the rotor wall (canvas lined) is about 0.40 so if r=2m. v=5ms-1. What would be the angular velocity?
Since v=rω, &omega=7/2 =3.5 rad s-1. Revolutions per minute = (3.5 rads-1x60 sec)/2π rad=210/2π=105/π
Looping the Loop
Consider a bucket of water when it is at the top of the loop A. If the weight of the water mg is less than mv2/r, the normal force N of the bottom of the bucket on the water. However, if the bucket is swung more slowly than mg will mv2/r and the residual part of the weight causes the water to leave the bucket.
Centrifuge and Washing Machines
Clothes get damaged in the washingmachine because the clothes experience a high force of gravity
Space Elevator
One application of centripetal force and circular motion is found in the space elevator lift. It was proposed by Russian scientist, Yuri Artsutanov in 1960 as a possible way of getting into space. It works on the principle that at a object orbiting the Earth above the equator with a period of 24 hours will remain in the same position above the Earth (see geostationary satelites). If a rope were to be lowered from the object, then an elevator car could climb up the rope into space without the need for a rocket. Since the rope has mass the additional weight of the rope would cause the satellite holding it to be pulled back to Earth. However, a counter weight orbiting the Earth a greater distance than the geostationary height would be travelling faster to stay in the same position over the equator the centripetal force of the counterweight can be balanced against the weight of the rope. The result is that the rope stays in place and the space elevator becomes possible.
Even though the theory is sound, there are significant technical challenges yet to be overcome before the space lift becomes a reality. The first is to do with the material properties of the rope. Given that the height of the geostationary orbit is some 3.58 x 104 km above the equator, any rope would have to be extremely strong to support its own weight. At present there is no known material that would be able to support its own mass at this length however, carbon-nanotubes have been suggested as a possible material for such ropes because of their low mass per unit length and extreme strength.
Other problems such as space debris also need to be overcome.
