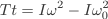Angular Momentum

In linear motion, it is often useful to consider the (linear) momentum of a body in rotation motion, angular momentum is important. Consider a rigid body rotating about an axis O and having angular velocity ω at some instant. Let A be a particle of this body distance r₁ from O and having linear velocity v₁ then the linear momentum of A is m₁v₁=m₁r₁ω. The angular momentum is important. Consider a rigid body rotating about an axis O and having angular velocity ω at some instant. Let A be a particle of this body distance r₁ from O and having linear velocity v₁ then the linear momentum of A is m₁v₁=m₁r₁ω. The angular momentum of A about O is defined as the moment of its momentum about O. Hence, angular momentum of A=r₁m₁ωr₁=ωm₁r₁². Therefore, total momentum is

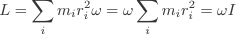
$L=\sum_{i}m_{i}r_{i}^2\omega=\omega\sum_{i}m_{i}r_{i}^2=\omega{I}$

Work Done by Couple

Rotation is changed by a couple, that is, by two equal and opposite parallel forces whose lines of action do not coincide. It is often necessary to find the work done by a couple so that the energy transfer occuring as a result of its action on a body is known. Consider the wheel of radius r in the figure, on which the two equal and opposite forces P act tangentially and rotation through an angle θ occurs. Work done by each force = force x distance

P arc AB= Prθ

Total work done by couple = Prθ+Prθ= 2Prθ

But torque (or moment) of couple= torque x angular-rotation.

$W=T\theta$

In general, if a couple of torque, T about a certain axis acts on a body of moment of inertia I through an angle θ about the same axis and its angular velocity increases from O ro ω then,

Work done by couple = kinetic energy of rotation

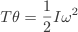
$T\theta=\frac{1}{2}I\omega^2$

Newton's 2nd Law

A body rotates when it is acted upon by a couple. The rotational form of Newton's 2nd law of motion may be written (by analogly with F=ma).

$T=I\alpha$

Conservation - a similar argument to that used to describe the principle of conservation of linear momentum from Newton's third law can be employed to derive the principle of conservation of angular momentum. Consider angular impulse = rate of change of angular momentum.

Site Search