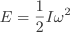Moment of Inertia
In the cases considered so far we have treated the body as a particle so that 'all of it' revolves in a circle of the same radius. When this is not realistic we have to regard the rotating body as a system of conserved 'particles' moving in circles of different radii. The way in which the mass of the body is distributed then effects its behaviour.
This may be shown by someone who is sitting on a freely rotating stool with a heavy weight in each hand. When he extends his hands the speed of rotation decreases but increases when he brings them closer to his body. The angular velocity of the system is clearly dependent on how the mass is distributed about the axis of rotation.
The mass of a body is a measure of its built-in opposition to any change in linear motion. i.e. mass measure inertia. For rotational motion, the coresponding property is called moment of inertia. The more difficult it is to change the angular velocity of a body about a particular axis. The greater is its measure of moment of inertia.
Experiment shows that a wheel with most of its mass in the rim is more difficult to start or stop. Similarly, the person on the swivel chair, has a greater moment of inertia when their arms are outstretched than when there hands are close to their body. We shall find out by considering the kinetic energy of the rotating body
Kinetic Energy of a Rotating Body
Suppose the body is rotating about an axis through O with a constant angular velocity ω. A particle A of mass m, at a distance r1 from O describes its own circular path. If v1 is its linear velocity along the tangent to the path, at the instant shown then v1=r1ω and the kinetic energy of A=(1/2)m1v12=(1/2)m1v12ω2
It follows that the kinetic energy of the whole body is the sum of the kinetic energy of its component particles. If these have masses m1, m2, m3, etc. and are distributed at distances r1, r2, r3, etc. from O then since all the particles have the same angular velocity (the body is rigid).
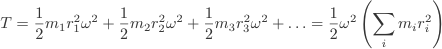
The quantity ∑miri represents the sum of the mr2 values depends on the mass and distribution of and is taken as a measure of the moment of inertia of the body about the axis in question. It is denoted by the symbol I.
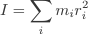
Therefore, the rotational K.E. of the body is