Centre of Mass

The centre of mass, also known as the centre of gravity is the point at which an object can be treated as being effectively a point mass. It is also the point at which an object will balance from. It is especially useful because the real motion of object can be quite complicated. It might be a rotating and spinning as it travels, for example, a sommersaulting motocross bike getting some air-time across a wide gap. At the centre of mass, the bike and rider behave as a point particle and the more simple rules of projectile motion apply.

To calculate the centre of mass we break the object into much smaller masses and sum the product of each smaller mass and its vector distance from a reference point choosen to be the origin and divide that by the sum of individual masses. (This is actual the total mass).

$${\vec{r}_{cm} = \frac{\sum_i m_i \vec{r}_i}{\sum_i{m_i}}=\sum_i\frac{m_i \vec{r}_i}{M}}$$

This vector equation reduces to:

$${x_{cm}=\sum_i\frac{m_i x_i}{M}}$$

$${y_{cm}=\sum_i\frac{m_i y_i}{M}}$$

$${z_{cm}=\sum_i\frac{m_i z_i}{M}}$$

To consider a continuous system, we think about the particles that make up the object becoming progressively smaller and smaller. At the point where they become infinitesimally small we can replace the sum by an integration over the volume of space.

$${\vec{r}_{cm} =\frac{\int{\vec{r}_i}dm}{\int{dm}}}$$

Which of course translates to three separate equations.

$${x_{cm}=\frac{1}{M}\int x dm}$$

$${y_{cm}=\frac{1}{M}\int y dm}$$

$${z_{cm}=\frac{1}{M}\int z dm}$$

Experimental Determination of Centre of Mass

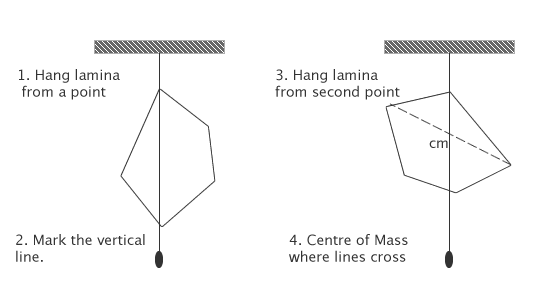
It is usually quite easy to determine the centre of mass for a simple geometic object such as a square or triangle. If the density of the material is constant then it is at the centre of the object. However, for an irregular shaped object made of different materials with different densities then it would be more problematic. Luckily, there is a simple method that will allow you to find the CM with a few measurements. This method works best for flat objects, technically known as lamina, otherwise the centre of mass would be hidden inside the object.

The object is hung at single point from piece of string. The centre of mass of the object will create a moment about the point the object is hung from, which will reach an equilibrium position where the centre of mass will be some point below the string. At this stage, the centre of mass is not fully determined, however. It could be anywhere on the vertical line downward from the point of suspension. If this line is marked, and then the object is suspended from a completely new point, the object will come to rest in a new equilibrium position and the centre of mass will also be on this line. For a lamina object, the lines should meet at a point. This is the centre of mass. For an extended object, the centre of mass is still not uniquely determined. Suspension of the object is required to find the CM and it will be inside the object.

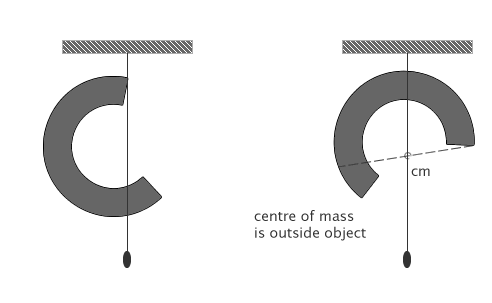
However, the centre of mass doesn't have to be inside the object. If the object has a strange shape where most of the mass is around the outside and it is curled up, the centre of mass can be at a point in space.

Fosbury Flop

Athletes in the high-jump take advantage of this fact in the so called Fosbury flop. (after the American high-jumper Dick Fosbury). To leap over the bar, it would normally require that the athlete haul their entire body, including their centre of mass over the bar.

However, by jumping such that their entire body arches over the bar, the centre of mass is moved outside of the athlete's body and in fact the centre of mass actually passes under the bar. As a result, the athlete can jump over a higher bar for the same amount of effort, compared to using the conventional high-jump technique.