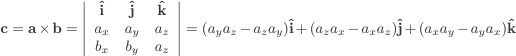Scalars and Vectors

Introduction

Some physical quanties can be expressed by a single number, such as mass, temperature, volume, voltage, energy, pressure and charge. These are known as Scalars. Vector quantities need both a magnitude and direction. Examples include velocity, force, momentum, angular velocity and electric field.

Vectors

If we are in a large room at point A and I move ten metres in straight line to point B then this can be represented as a vector. Starting from point A and moving in a new direction and moving 10 metres in a different direction results in a new vector AC.

Since the vector has direction we cannot specify it with one number, we need to define the position of the endpoint from some origin.

Notation

Vectors are usually distinguished from scalar values by writing them in boldface. When writing them on paper, we usually denote them with an arrow or line above the letter. Eg, a or a.

Vector Components

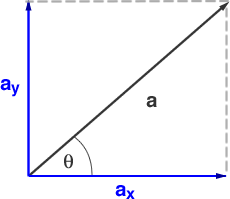
A single vector can be decomposed into two independent vectors in the same the direction as the coordinate axes. These are known as the components of the vector. The mqgnitude of the horizontal component is |a_x| = |a| cos θ and the magnitude of the vertical component is |a_y| = |a| sin θ, where θ is the angle between the vector a and the horizontal axis

Figure. Vector and its components.

Vectors provide a shortcut when thinking about equations in more than one dimension, we can write F = ma to describe the force but in reality we are thinking about three equations,

F_x = ma_x

F_y = ma_y

F_z = ma_z

Where F_x, F_y and F_z are the three components of the vector F in the x, y and z directions respectively and a_x, a_y and a_z are the three components of the vector a in the x, y and z directions respectively. Sometimes we can reduce the problem to one dimension and we can drop the vector notation.

Unit Vectors

The components of a vector are in the same direction as the axes of the coordinate system, if they are of unit length then they are also unit vectors in the direction of the axes.

Addition

Head to Tail Rule

Figure 1. Head to tail addition of vectors

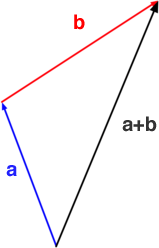
Two vectors can be added together to make a new vector. Graphically, this is done by moving the head of one of the vectors up to the tail of another. A line drawn from the tail of one to the head of the other is the resultant.

Parallogram Rule

Figure 2. Parallelogram addition of vectors

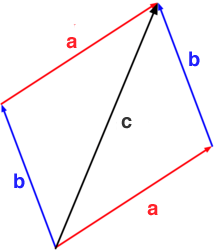
Writing Vectors

While drawings are great for showing the concept of vectors, drawing arrows to scale quickly becomes tedious and so we seek a less tiresome way to represent vectors. Luckly, we can also write vectors algebraicaly in terms of their components. Thus a vector may be written as a coordinates (x,y) which gives the position of the tip of the arrow from the origin. If we wish to use more than 2-dimensions we can simply add another component to the list. Alternatively, we may represent the components of a vector as a multiple of a vector with unit distance. These multiplying vectors are known as unit vectors. Conventionally, they are denoted by i and j (also k in 3-D). In this way, a vector a may be represented as a=xi + yj. Where x and y.

Two vectors add to produce another vector.

c=a+b

c=(a_xi + a_yj) + (b_xi + b_yj)

c=(a_x+b_x)i + (b_x+b_y) j

Subtraction of vectors is treated in a similar way. So that, c=a-b

c=(a_x-b_x)i + (b_x-b_y) j

Magnitude

Having defined the vector in space how do we find out its length when it is pointing anywhere? At this point we remember, Pythagoras whose theorem, (he dihttdn't discover it) we need to obtain the distance. The components of a vector are perpendicular to each other and therefore we can determine the length of the vector from these.

Pythagoras's theorem is c²=a²+b². Where a and b are the perpendicular to each other and c is the hypoteneus.

Figure. Vector and components to determine magnitude.

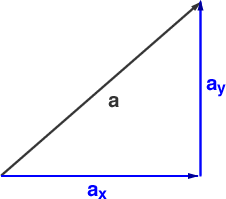
Relating this to the vector, the magnitude of vector a is then |a|=√(a_x²+a_y²). We use the | lines around the vector to indicate the magnitude.

Direction Cosines

Dot Product

The dot product or scalar product is a special form of multiplying a vector. The dot product gives the projection of the vector onto the x-axis. It is represented by a dot between the two vectors one is multiplying, a.b. The result is not a vector but a scalar. a.b=|a||b| cos θ

Figure. Scalar product of two vectors a and b.

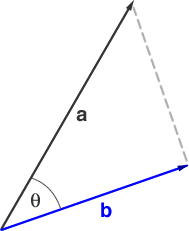
Also, a.b=a_x.b_x+a_y.b_y+a_z.b_z. They both give the same result however, the latter may sometimes be more conveinient if one doesn't known the angle between the two vectors.

Vector Product

The vector product is the other form of multiplication of vectors the result of a vector product is another vector that is perpenducular to the two vectors being multiplied. To obtain the vector product we must move into three-dimensional space.

Figure. Vector product of two vectors a and b.

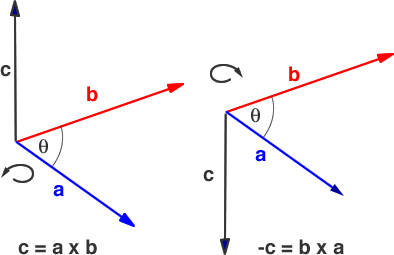
We always work in a right-handed coordinate system. (ie the crossproduct of a and b is 1. a x b =c) and it is a good idea to draw the axis to make it clear.