Velocity and Speed
If we measure the time it takes for an object to move from one point to another we can determine how quickly it is moving. In everyday language, speed and velocity are often used interchangably but in physics they have a precise meaning.
From the last section we learnt about distance and displacement and their definitions lead to two different ways we can define how an object moves with time.
The velocity of an object is defined as the change in displacement with the change in time. v = Δs/Δt. Since displacement is a vector quantity the velocity is also a vector with both magnitude and direction.
The speed of an object is defined as the distance travelled Δs divided by the time period Δt taken to travel that distance. It is a scalar quantity.
v = Δs/Δt
Quite often, you will see graphs plotted of displacement plotted against time like the one below:
Displacement-Time Graphs
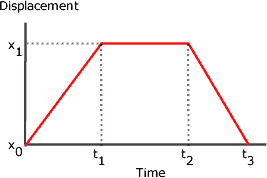
The graph in Figure 1. shows an idealised graph of displacement plotted against time for some imaginary object moving in 1-dimension. It starts off at a point x0, at time t0 at travels to a point x1 at t1. It then stops moving for a while until at t2 it starts moving again and returns back to its original position at t3.
We can calculate the object's velocity in each one of the regions by using the change in displacement divided by the time taken. To put some numbers in, suppose that the time taken to travel from from t0 to t1 was 5 seconds and in that time, the object travelled 10 metres. The velocity would be 10 m / 5s = 2 m/s. We have choosen the vertically upward direction to be positive so the velocity is positive.
Let us say that the time interval from t1 to t2 is 5 seconds. In this time, the object was stationary so the velocity was zero [(x1 - x2)/5 s = 0 m/s]. Finally, in going back to its starting position, it moved -10 m and if it did it in 3 seconds, its velocity would be -10 m / 3 s = -3.33 m/s. (Notice that we were talking about velocity so we use the displacement which is negative in this time period. The speed from x2 to x3 would be 3.33 m/s)
It so happens that because this is a simple displacement-time graph, the object is moving with constant velocity and so the velocity measured in each time interval did not change within each period of time but in general this is not usually the case. More realistically, the object will change its velocity the time interval, especially if measuring the displacemeny over a large time interval. What we are measuring in this case is the average velocity or average speed if measuring the distance travelled.
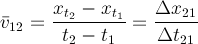
The line over the v indicates an average or a mean and the delta symbols indicate a difference or a change. If we want to get a more representitive value of the velocity at a specific time we need to measure the change in displacement over smaller time intervals. The measured velocity becomes closer to the instantaneous velocity.
Mathematically, this idea is encapsulated as the limiting case of taking a time interval, over which the change in position is being measured, which tends to zero. We call this the rate of change of position with respect to time or the derivative of position with respect to time. It is a very important idea.
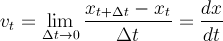
Summary of Average and Instantaneous Speed and Velocity
| Equations for Speed | ||
| average | 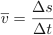 |
|
| instantaneous | 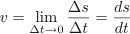 |
|
| Equations for Velocity | ||
| average | 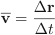 |
|
| instantaneous | 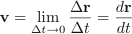 |
|
Speed and velocity are related in much the same way that distance and displacement are related. Displacement is measured along the shortest path between two points and thus its magnitude is always less than or equal to the distance. The magnitude of the displacement approaches the distance as distance approaches zero. That is, distance and displacement are effectively the same (have the same magnitude) when the interval examined is "small". Since speed is based on distance and velocity is based on displacement, these two quantities are effectively the same (have the same magnitude) when the time interval examined is "small" or, in the language of calculus the magnitude of an object's average velocity approaches its average speed as the time interval approaches zero.
Δt → 0 ⇒ v → |v|Thus, the instantaneous speed of an object is the magnitude of its instantaneous velocity. v = |v|
Fastest and Slowest
Speed of Light
The fastest speed that anything can move is the speed of light, c. A photon of light, in a vacuum travels at 2.997924580 x 108 m/s. It is magnitude is exactly predicted by Maxwell's equations and is the result is a combination of two physical constants that have to do with electric and magnetic properties.
Particle Accelerators
Particle accelerators can accelerate sub-atomic particles to a fraction of the speed of light but as they get closer to the speed of light, the mass of the particle increases and so more and more energy is required to them closer and closer.
Helios 2
The fastest extended man-made object is the space-probe, Helios 2. It was designed to measure processes that occur on the Sun. The maximum speed of Helios 2, which was achieved at its perihelion distance of 0.29 AU on 17 April 1976, is quoted as about 150,000 mph (241,350 km/h). This is still only 0.022 % of the speed of light, so some way to go before we can create spacecraft that can travel near to the speed of light.
Hyper-Velocity Hydrogen Gas Gun
Hydrogen gas guns are used for studying high-velocity impacts. A conventional gun uses an explosive charge to create the region of high pressure gas that accelerates a projectile down the barrel. The limiting factor in the projectile's speed is the speed in which a pressure wave can travel through the gas.
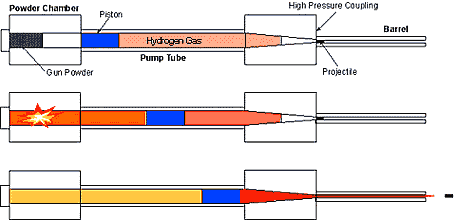
The speed of sound in Hydrogen gas is around 3.8 times that of the speed of sound in air. The speed of sound also increases with temperature. In the Hydrogen gas gun, a convention explosive charge sends a piston down the barrel filled with hydrogen gas. This compresses hydrogen gas in a pressure chamber and heats it. The hydrogen is prevented from escaping by a burst disc which is calibrated to break at a specific pressure. When the hydrogen is compressed beyond this limit, the disc bursts and the projectile is accelerated down the barrel. A hydrogen-gas gun can shoot a projectile at about 7km/s while the fastest conventional guns can shoot a projectile at 1.2-1.5 km/s.
Second-Class Post

Among the slowest objects in the universe are sent by second-class post. You might think I am being flipant but there is some truth in it. There are quite a few instances of post being delayed for decades. One instance is of a postcard, sent in 1916 by a soilder in the First World War, who wrote to his sister before being sent off to fight in the trenches. It took 94 years to travel from Newhaven, East Sussex to reach its recepient in Norwich, Norfolk, a distance of around 150 miles, meaning its average speed was (1600 x 150)/(3600 x 24 x 365.25 x 94) = 8 x 10-5 m/s. By the time the postcard arrived the sister had died and the house was occupied by a new owner.
Finger Nails
Finger nails grow at a rate of about 3 mm a month or 0.003 m/(365.25/12 x 24 x 3600) s = 1 x 10-9m/s =1 nm/s. Of course this is the average speed. In fact the rate at which fingernails grow is more interesting. An experimental study, in 1979, in The Journal of Investigative Dermatology, among other things, it showed that i) finger nail growth rate slows as you age and male fingers nail grow more than more than females until about 60 years old, then female nails grow more than males.
ref: http://www.nature.com/jid/journal/v73/n1/pdf/5616254a.pdf
Continental Drift
The plates of the Eurasian plate is moving away from the North American plate at a velocity of about 2cm per year. or around 0.02/(3600 x 24 x 365.25) = 6.3 x 10-10 m/s.
