Integration
Introduction
Integration is a major parts of calculus. It is an extension of the concept of summation. In fact the integration symbol derrivesfrom an elongated letter S, first used by Leibniz, to stand for Summa meaning sum in Latin.
Integration is widely used throughout mathematics and physics and so is an important concept to grasp. In fact you can't really do any serious physics without knowing about it.
The Area Under a Curve
One way of understanding integration is to see how it is used to find the area under a curve defined by a function f(x). Imagine trying to find the area under a curve.
Clearly, this is a very poor approximation but we could do a little better by adding together the area of two rectangles of half the widths with different heights corresponding to the value of the function at the points where corner meets the function.
We define an interval [a,b] which is divided into n equal parts. Δx = (b-a)/n.
x0 = a, x1 = a+Δx, x1 = a+ 2Δx, ... ,xn = a+nΔx = b
Having partitioned the interval into n equal parts, the area of the kth strip is Δx f(xk), where f(xk) is the value of the function at the xk. Summing all the areas of all the strips gives the approximate area under the curve. The left-Riemann sum starts with the zeroth strip and ends at the (n-1)th strip. In this case resulting area will be an under-estimate of the true area.
Left-Riemann Sum
Al = f(x0)Δx + f(x1)Δx + ... + f(xn-1)Δx
= [f(x0) + f(x1) + ... + f(xn-1)] Δx
= Σn-1k=0f(xk) Δx
We could also have represented the area by starting our summation of rectangles at k=1 and endding at k=n. This known as the right-Riemann sum. In this case, it over-estimates the area under the curve.
Right-Riemann Sum
Ar = f(x1)Δx + f(x2)Δx + ... + f(xn)Δx
= [f(x1) + f(x2) + ... + f(xn)] Δx
= Σnk=1 f(xk) Δx
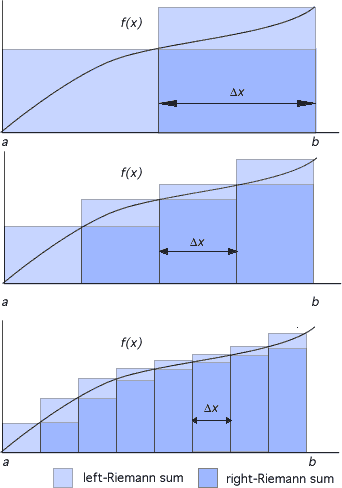
As the number of strips increase, the value of Δx decreases. In the limit, Δx tends to zero as n tends to ∞. The areas calculated by the left and right Riemann sums become closer to the true value of the area. In the limit, the sum becomes the definite integral of f(x).
Σ∞k=0f(xk)Δx = ∫baf(x) dx
The accuracy for larger rectangles widths can be improved by choosing the mid-point of each rectangle, to corespond to the value of the function at that point. An overestimate is cancelled out to some degree by the underestimate.
Definite and Indefinite Integrals
Definite Integrals
The integration symbol sometimes has numbers or other letters alongside the integral sign. These are called the the limits of integration, the top one is known as the uppper limit and the bottom one is the lower limit.
Essentially, these numbers are substituted into the integral after the integration has been performed. For example
f(x) = ∫72x2 dx
The integral of the term x2 is x3/3. The value of the top limit is substituted in for x in the result. Therefore, 73/3 = (343/3). Next the lower limit, 2, is substituted for x giving, 23/3 = 8/3.
The final result is given by taking the first limit from the second. So (343/3) - (8/3) = 335/3 = 111.3333'
Indefinite Integral
Where there are no limits on the integral sign, the integral is called indefinite, meaning there is no specific value. Rather, the result is a family of functions. The integration is performed in the same way but we must remember to add an arbitrary constant known as the constant of integration. For example,
∫x2 dx = x3/3 + C
Why is this? If we take our answer x3/3 and differentiate with respect to x, we obtain x2. We would also obtain the same answer for x3/3 + 5 or x3/3 - 2 or x3/3 + any constant. Therefore, when we integrate, we have to add a constant because differentiation of a constant is zero.The value of the constant has to be determined by additional information about the equation, for example where it intercepts the y-axis.
Common Integrals
|
∫k f(u) du = k ∫f(u)du ∫[f(u)±g(u)] du = ∫f(u) du ± ∫g(u) du ∫du=u + C ∫un du = un+1/(n+1) + C, (n ≠ -1) ∫du/u = ln|u| + C ∫eu du = eu + C ∫sin(u) du = - cos(u) + C ∫cos(u) du = sin(u) + C ∫tan(u) du = - ln|cos(u)| + C ∫cot(u) du = ln|sin(u)| + C ∫sec(u) du = ln|sec(u) + tan(u)| + C ∫cosec(u) du = ln|cosec(u) + cot(u)| + C ∫sec2(u) du = tan(u) + C ∫cosec2(u) du = -cot(u) + C ∫sec(u) tan(u) du =sec(u) + C ∫cosec(u) cot(u) du = - cosec(u) + C ∫(a2 - u2)-1/2du = - arcsin(u/a) + C ∫(a2 + u2)-1/2du = (1/a) arctan(u/a) + C ∫(a2 - u2)-1/2du = - arcsin(u/a) + C d/dx[∫xaf(t)dt] = f(x) |
Integration by Substitution
The substitution of a function, may simplify the integral allowing it to be calculated easily.
Examples
∫215x2 cos(x3) dx
Try u = x3, therefore, du = 3x2dx.
x2dx = (1/3) du
We must change the limits of integration, the new values come from u = x3, therefore when x= 1, u = 1 and when x= 2, u = 8. The integral becomes,
∫81(5/3) cos(u) du
(5/3) sin(u)|81 = (5/3)[sin(8) - sin(1)]
Integration by Parts
Let U and V be functions of x. From the product rule:
d(UV)/dx = V (dU/dx) + U (dV/dx)
Integrating both sides with respect to x and rearranging,
∫ U(dV/dx).dx = UV - ∫ V (dU/dx) dx
Given some product to integrate, we arrange for U and dV to make the integral on the right-hand side, V(dU/dx) more simple than the integral U (dV/dx) we started with.
Example
∫x exp(-x) dx
Let u =x, dv = exp(-x), therefore du = dx, v = -exp(-x)
∫x exp(-x) = -x exp(-x) + ∫-exp(-x) dx =
-x exp(-x) - exp(-x) + C
The Fundamental Theorem of Calculus
Integration is the inverse process of differentiation.
∫baf(x)dx = F(b)- F(a)
dF(x)/dx = f(x)
Therefore if we recognise that the function to be integrated as a derivative, then we can say the integral is the function that gaves that derivative. For this reason we sometime call the integral the anti-derivative.