Differentiation
Differentiation or the derivative is the instantaneous rate of change of a function with respect to one of its variables. This is equivalent to finding the slope of the tangent line to the function at a point.
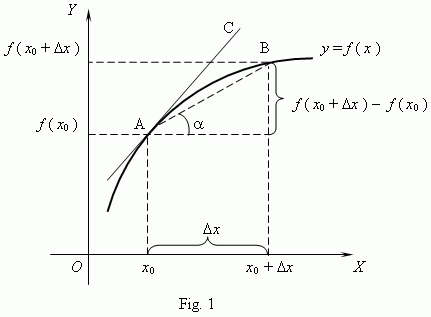
lim Δx→0 (f(x0+Δx) - f(x))/Δx = df(x)/dx.
It is possible to haves differentiate the function f(x) more than once. The second-derivative is the derivative of the derivative of a function.
Notation
There are many popular notations for writing the derivative. The usefulness of each notation varies with the context and it is sometimes advantageous to use more than one notation in a given context. The most common notations for differentiation are listed below.
Leibniz's Notation
Leibniz's notation, is d dx f(x).
The second derivative d2dx2f(x)
and Higher orders of differentiation are shown as dndxn f(x)
Lagrange's Notation
Lagrange's notation is a common notation and perhaps a more convinient form for writting in HTML. It denotes the derrivative by a superscripted prime mark '.
For example, f ' for the first derivative. Higher order derivatives up to the third order, are written by adding prime-marks. Thus f '' and f ''' are written for the second and third order, respectively. Even higher orders may be represented by an arabic number in brackets. f (n) is the nth derivative.
Newton's Notation
x . for the first derivative.
x .. for the second derivative.
x... for the third derivative.
Euler's Notation
Euler's notation is represented by a capital D. For example, Dx2f(x).
General Power Rule
If we have some function of f(x) = xn where n is a integer.
dxndx = n xn-1
Example
Differentiate, x3, 4x3, 4x2-6x + 6
Answers:
3x2, 12x2, 8x - 6
Chain Rule
Given f(x) which is a function of another function g(x). Then h(x)=f(g(x)). The derivative is given by the chain rule:
h'(x) = g'(f(x)) f'(x)
Examples
Differentiate the following functions with respect to x
i) (3x5 + 9x3 + 3x2 -62)2
Answers
-
2 (15x4 + 27x2 + 6x) (3x5 + 9x3 + 3x2 - 62)
90x9 + 432x7 + 126x6 + 486x5 - 1590x4 + 36x3 - 3348x2 - 744x
Product Rule
The chain rule allows us to differentiate, a product of terms that depend on the differentiation variable. For example, U(x) and V(x) are function that depend on x. Then the differential is given by:
d dx (UV) = U dVdx + V dUdx
Quotient Rule
Where we have a quotient, the rule for differentiation is
d dx (U/V) = [V dUdx - U dVdx ]/ V2
Other Functions
Differentiation of trigonometric and other functions
| f(x) | f '(x) |
|---|---|
| x | 1 |
| 1/x | -1/x2 |
| exp(x) | exp(x) |
| exp(ax) | a exp(ax) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| cosec(x) | -cot(x)cosec(x) |
| ln(x) | 1/x |