Waves
This section just covers the basic terminology associated with waves. A wave is an oscillation that transfers energy from one point to another in space. Waves can be classified into two types:
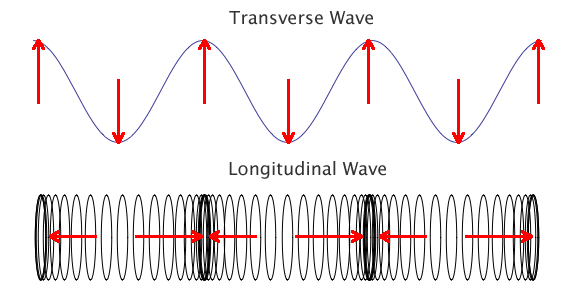
Transverse - the displacement of the wave is perpendicular to the direction of travel.
Longitudinal- the displacment is in the same direction as the direction of travel.
However, they can both be described by the same general equation.
The general equation for a wave as function of position $x$ and time $t$ is given by:
$${y(x,t) = A_0\cos(k x - \omega t + \phi)}$$
Where $A_0$ is the Amplitude, which is the vertical distance from the centre of the wave to a peak or trough. $k$ is the wavenumber or sometimes called the wave vector this is really a constant that is associated with how fast the wave cycles with position $x$. $\omega$ is the angular frequency and is another constant that tells us how fast the wave cycles with time $t$. Finally, $\phi$ is called the phase and defines at what point in cycle the wave starts at. Depending on the application, the position dependent arguments, time dependent argument or the phase might be omitted to simplify things.
Some authors, use the sine function but they are both equally valid since, $\sin(\theta)\equiv\cos(\theta+\pi/2)$ and amount to a difference in phase angle. Another useful form is the exponential form, in which the exponential function to the power of the complex number $i$ is used.
$${y(x,t) = A_0\exp(i(kx -\omega t)+\phi)}$$
$${\exp(i\theta)\equiv\cos(\theta)- i\sin(\theta)}$$
and usually we only need the real part of this.
In two-dimensions or three-dimensions, the spatial parts of the argument become vectors. For example in this three-dimension wave.
$${\Psi(\vec r,t) = \vec A_0\cos(\vec k .\vec r - \omega t + \phi) \equiv}$$
$${(A_x\exp(i(kx -\omega t+\phi))\;,\; A_y\exp(i(ky -\omega t+\phi))\;, \; A_z\exp(i(kz -\omega t+\phi)))}$$
The period of a wave is the time that it take to complete one cycle.
$${T=\frac{1}{f} = \frac{2\pi}{\omega}}$$
The frequency is given by:
$${f = \frac{\omega}{2\pi}}$$
and the wave number $k$ is:
$${k = \frac{2\pi}{\lambda} = \frac{2\pi f}{c} = \frac{\omega}{c}}$$
The velocity of the wave is related to the frequency and wavelength.
$${c = f \lambda}$$
