The Wave Equation

What would like to calculate an equation which tells in general something that gives us the relationship between the forces acting on a string and the way in which the particles move.

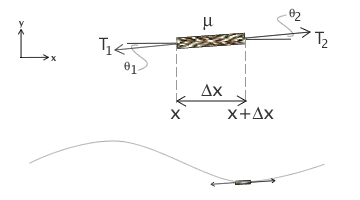
Consider a string that is stretched accros a gap and then plucked, as shown in Fig. 1. The diagram shows the general state of some small element of the string, it has tension forces $T_1$ and $T_2$, acting in opposite directions. The mass of the of the string is given in terms of its mass per unit length $\mu$. For the analysis we consider an elemental part of string of length $\Delta x$ at the point it is released. Since the string is not moving in the x-direction, we do not need to worry too much about the forces in the x-direction, but instead consider the forces acting in the y-direction.

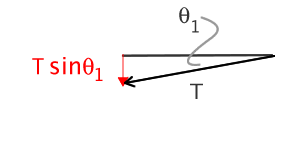
The sum of the forces in the y-direction: $F_{y}= T_{2} \sin(\theta_{2}) - T_{1}\sin(\theta_{1})$

From the relationship, $\frac{\sin(\theta)}{\cos(\theta)} =\tan(\theta)$, $${\sin(\theta) =\cos(\theta)\tan(\theta)}$$

We obtain,

$${F_{y}= T_{2}\cos\theta_{2} \tan(\theta_{2}) - T_{1}\cos(\theta_{1)} \tan(\theta_{1})}$$

We make use of a couple of approximations. Firstly, that the angles $\theta_1$ and $\theta_2$ are small, so that $\cos(\theta)$ will be very close to 1. Secondly, the tension forces are about equal, so we make $T_1$ and $T_2$ equal and call it $T_0$.

This reduces the force equation to:

$${F_{y}= T_{0} \tan(\theta_{2}) - T_{0} \tan(\theta_{1})}$$

We can replace the $\tan$ function by the by the slope in terms of the

$${T_{0}(\tan(\theta_{2}) - \tan(\theta_{1})) =T_{0}(\frac{dy(x+\Delta x)}{dx} - \frac{dy(x)}{dx}) = T_{0}\frac{d^2 y(x)}{dx^2}\Delta x}$$

We remember that this is also a function of t so we make the total derrivatives, into partial derivatives meaning that we differentiate with respect to $x$ but keep $t$ constant. The total forces in the y-direction are thus:

$${F_{y}= T_{0}\frac{\partial^2 y(x,t)}{\partial x^2}\Delta x}$$

This resultant force also is given by Newton's second law , $F=ma$, where $a$ is the second derivative of the position multiplied by the mass. And the mass is the mass per unit length, $\mu$ multiplied by the length of the string $\Delta x$.

$${F_{y} = \mu\Delta x a}$$

However, the acceleration can be defined as the second-derivative of position, so a becomes:

$${a = \frac{d^2y(t)}{dt^2}}$$

Not forgetting that $y$ is also a function of position $x$ so once-again we replace the total-derivative with the partial-derivatives.

$${a =\frac{\partial^2 y(x, t)}{\partial t^2}}$$

Putting this all together gives,

$${\frac{\partial ^2 y(x,t)}{\partial t^2} = \frac{\mu}{T_0}\frac{\partial ^2 y(x,t)}{\partial x^2}}$$

The wave equation can be written in a more general form, in terms of $c$, the velocity of the resulting waves.

$${\frac{\partial ^2 y(x,t)}{\partial t^2} = \frac{1}{c^2}\frac{\partial ^2 y(x,t)}{\partial x^2}}$$

For waves on a string with tension $T_0$ and a mass per unit length of μ, the $c^2$ constant gives the velocity of the waves as:

$${c=\sqrt{\frac{T_0}{\mu}}}$$

The solution admits any function that is a f(x±c t) and even any linear combination of

$${y(x,t) = c_{1} f(x\pm u t) + c_{2} g(x\pm v t)}$$

Where $c_1$ and $c_2$ are real valued constants, as can be verified by differentiating twice with repsect to $x$, and $t$. This is known as the principle of superposition

The wave equation is very important in many areas of physics and so time understanding it is time well spent. It crops up in many different areas of physics from electromagnetism, optics to quantum mechanics, understand the mathematics of waves and you understand a lot of physical phenomina.