Radioactivity
Introduction
In 1896, Bequerel, a French physicist discovered that crystals of Uranium salts emitted penetrating rays similar to X-rays which could fog photographic plates. Two years after this Pierre and Marie Currie discovered other elements: Polonium and Radium which had this property. The emission was known as Radioactivity.
The Stability of Nuclei
Protons and Netrons are held together in the nucleus of an atom by the strong-force. This force acts over a very short distance of about ~1 fm, (10-15m) and over this short distance it can overcome the electromagnetic repulsion between the positively charged protons. Nuclei with radii that are within the range of the Strong force are stable. As atomic number increases the radius of the nucleus also increases and the element becomes unstable. This instablity manifests itself as the emission of particles or energy from the nucleus. The elements with atomic number greater than 82 are radioactive.
The Decay Constant
The decay constant is a measure of how quickly on average a radioactive nuclei will take to decay. Since radioactive decay is a random process, the decay of a single nucleus may happen at any time but for many undecayed nuclei, the average decay rate is given by the decay constant, λ and it has the unit of [s-1] or [h-1] or [year-1].
Activity
The activity of a radioactive material is defined by two factors:
- the number of undecayed atoms, N
- the decay constant, λ
The activity, A is measured in Becquerels [Bq] or [s-1].
A=λN
The corrected activity is the activity taking into account the background radiation.
Radioactive Decay
Consider a block of radioactive material, initially the number of undecayed nuclei is, N0. On the basis of our reasoning above we can say that the number which will decay will depend on overall number of nuclei, N, and also on the length of the brief period of time. In other words the more nuclei there are the more will decay and the longer the time period the more nuclei will decay. Let us denote the number which will have decayed as dN and the small time interval as dt. So we have reasoned that the number of radioactive nuclei which will decay during the time interval from t to t+dt must be proportional to N and to dt. In symbols therefore: -dN∝Ndt.Turning the proportionality in this equation into an equality we can write: -dN=λ N dt
Dividing across by N we can rewrite this equation as:
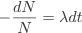
So this equation describes the situation for any brief time interval, dt. To find out what happens for all periods of time we simply add up what happens in each brief time interval. In other words we integrate the above equation. Expressing this more formally we can say that for the period of time from t = 0 to any later time t, the number of radioactive nuclei will decrease from N0 to Nt, so that:
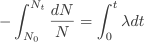
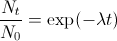
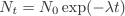
The final expression is known as the radioactive decay law. It has the form of an exponential decay curve like the one we saw in the discharge of a capacitor.
Radioactive Decay Simulation
The Flash animation below simulates the random decay of a small number of radioactive nuclei. Each atom nucleus has a constant probability of decaying. During the simulation, for each undecayed nucleus, a uniformly distributed random number is generated and if the number is less than the decay probability the atom will decay.
Initially the large proportion of undecayed nuclei will generate a large number of decays. As the number of undecayed atoms decreases, the number of decays will also reduce.
The red curve, shows the theoretical exponential decay curve for the array of nucleus plotting the number of undecayed nuclei against time. The blue curve is the simulated decay rate. Due to the statistical nature of the process there are small variations in the decay curves but overall the agreement is good.
The graph also shows the half-life of the decay process. In each half-life the remaining nuclei will reduce by a half from an initial number N0 to N0/2 in the first half-life, then to N0/4 in second half-life, N0/8 in the third, and so on.
Run the simulation several times to observe the statistical decay process.
Radioactive Decay Law with Sweets
You can simulate the decay process the next time you have a bag of M&Ms. Take the packet of M&Ms and empty them on a flat surface. The M&Ms which land such that you can see the 'M' represent the nuclei that have decayed. Since you can see the M or not the decay constant is 0.5 Record the number that of decays and you can eat the them. Repeat the process with the remaining M&Ms until there are no more remaining.
Starting with 50 M&Ms, the decay sequence is
| Throw | Theory | Actual |
|---|---|---|
| 1 | 50 | 50 |
| 2 | 25 | 25 |
| 3 | 12.5 | 12 |
| 4 | 6.25 | 8 |
| 5 | 3.125 | 3 |
| 6 | 1.5612 | 2 |
| 7 | 0 | 0 |
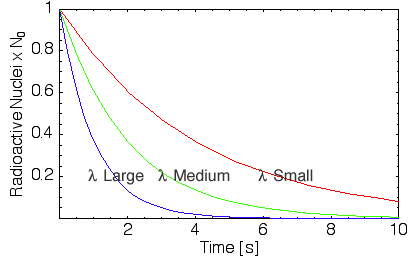
Half-Life
The decay law leads to an exponential decay which reaches zero in an infinite amount of time. A useful measure of rate at which the material decays is given by the half-life. This is the time taken for the number of undecayed nuclei to decrease by half the initial amount.
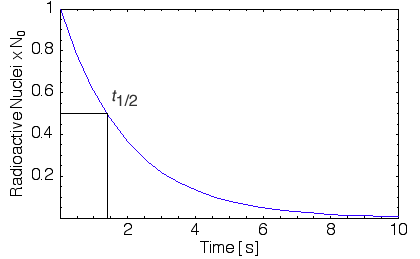
Successive half-lifes decreases the number of undecayed nuclei by N0/4, N0/8, etc. As shown in Figure X.
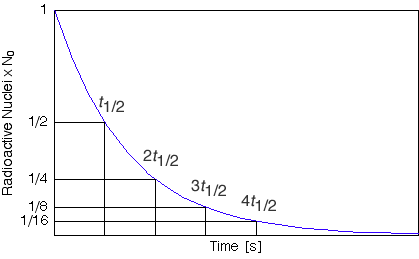
Mathematically, the half-life can be calculated by seting Nt=N0/2 in the radioactive decay equation. Therefore, N0/2=N exp(-&lambdat1/2). Taking logs and re-arranging for t1/2 leads to t1/2 = ln(2)/λ
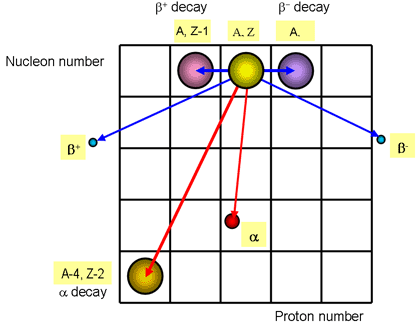
Modes of Radioactive Decay
There are broadly three types of radioactive emissions. These are:
α radiation
Alpha radiation is the emission of two protons and two neutron from the nucleus, which is the same as a Helium nucleus. Due to the heavy mass and charge, α radiation the least penetrating, being stopped by a sheet of paper. However it also is the most ionising form of radiation, knocking electrons from their shells in nearby atoms. The dangers of alpha-radiation come from being ingested into the body. When an alpha particle is emitted, the proton number decreases by 2 and and mass number decreases by 4.
AZX → A-4Z-2(X-2) + 42α
β radiation
.β radiation is the emission of an electron from the nucleus. Since the nucleus does not contain any electrons, either a proton or a neutron transforms. Depending on which transforms leads to one of two kinds of beta radiation.
Beta radiation occurs in two forms. β+ and β-
- β+ a positive electron called a positron is created by the transformation of a proton into a neutron.
AZX → AZ-1(X+1) + 0+1e+ + 00ν
- β- the electron is created by the transformation of a proton into a neutron.
AZX → AZ+1(X-1) + 0-1e- + 00ν;
The emission of the positron or electron is accompanied by the emission of a ghostly particle called a neutrino ν or antineutrino ν, respectively. Particle tracks photographed in a cloud chamber showed that the energy of emitted particles that showed up in the cloud chamber was not conserved. Rather than abandon the principle of the conservation of energy a new particle was postulated by W. Pauli in 1930. The lack of interaction between matter and neutrinos ment that it was 26 years latter the neutrino was discovered by Reines and Cowan with the anti-neutrino being found in
Beta radiation is more penetrating then α radiation but it can be stopped by a few mm of aluminium. Once again, the main danger of β radiation comes from when it is ingested in the body.
γ radiation
After the emission of an α particle or β decay, the nucleus is left in an excited state and it releases its excess energy in the form of a γ-ray photon. γ-rays are high-energy electromagnetic waves. They are also highly penetrating and are not stopped but the probability of absorption is proportional to the thickness of the absorbing medium, leading to an exponential decrease in the number of γ-ray photons passing through.
Transmutation