Geometric Optics
Light as Rays
For us to see something we need light. The light travels in straight lines and we use the concept of a ray of light to show the direction and path travelled by light. A light ray can be reflected off an object into our eyes or if it is luminous it emits rays of light in all directions and the light travels to the eyes.
A ray is the direction of the path taken by light and is represented in diagrams by a straight line with an arrow indicating the direction in which the rays is travelling
A beam of light is made up of many rays of light and may be parallel, divergent or converging.
Reflection from a flat Mirror
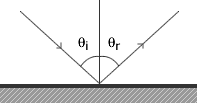
mirror. The angle of incidence is
equal to the angle of reflection.
When rays of light strike a flat mirror they are reflected and the exiting ray of light is reflected at the same angle as the angle of incidence. The angles of incidence and reflection are measured from a normal to the plane of the mirror as shown in Figure 1.
Reflection from a Diffuse Surface
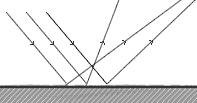
Some surfaces seem quite smooth; for example, a sheet of paper. However, we do see any reflections as with a plane-mirror. At the microscopic scale the law of reflection is obeyed but the surface is irregular which means the incident rays of light are reflected in many directions and the information contained in the in the light does not reach the eye in the correct order. This is known as diffuse reflection
Rotation of Plane-Mirror
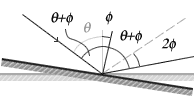
is twice the angle of rotation of
the mirror.
Consider a plane-mirror and a fixed incident ray of light reflecting from the surface at an angle θi. Before the mirror has rotated, the angle of incidence is θ as is the angle of reflection. If the mirror is rotated through an angle φ the normal is rotated by an angle &phi and thus the angle of incidence increases to θ +φ. Therefore, the angle of reflection must also increase by φ to θ+φ The difference between the final angle of reflection and the initial angle of reflection and is 2φ
For a fixed incident ray, the angle of the reflection is twice the angle through which the mirror has rotated. &thetaf= 2φ
Deviation of Light by a Plane-Mirror
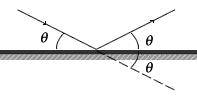
is twice the angle of incidence.
A ray of light that is incident on to the surface of a plane-mirror is reflected with the angle of incidence equal to the angle of reflection. Suppose that the ray had continued, through the mirror, in a straight line it would make an angle θ with the surface of the mirror. The total angle between the straight-line path and the reflected ray is twice the angle of incidence. This is called the deviation of the light and measures the angle at which the light has strayed from its initial straight-line path.
The deviation of a mirror is equal to twice the angle of incidence.