Nuclear Fusion
Introduction
Nuclear fusion is the process of binding nuclei together to form heavier nuclei with the release of energy. It is the process that powers the stars and of course our own Sun. Research into producing nuclear fusion on Earth began in the early 1950s with the development of the Hydrogen bomb. Research into nuclear fusion to generate electricity is ongoing despite the huge technical challenges. To put thing in perspective, to operate for a whole year generating about seven billion kilowatt hours of electricity, a fusion plant would use just 100 kg of deuterium and three tonnes of lithium - releasing no greenhouse gases in the process. A typical coal-fired power station, in contrast, devours three million tonnes of fuel and produces some 11 million tonnes of carbon dioxide to yield the same annual output.
Making Nuclei Stick
Atomic nuclei do not stick together easily. Protons have a positive electrical charge which prevents them combining with other protons. The repulsion is caused by the electromagnetic force between the two nuclei. However, at distances of 1015 m there is an attractive force which acts on the nuclei to keep them together and it is much stronger than the electromagnetic force. Appropriately, this force is called the Strong force. Over such short distances the strong force wins over the electromagnetic force and so the nuclei stay together. To create a situation where the nuclei have sufficient energy to overcome the electromagnetic force requires the nuclei to have extremely high kinetic energy and therefore, a high temperature.
We can estimate the temperature required to initiate fusion by calculating the Coulomb barrier which opposes the protons coming together. The magnitude of the force between protons is given by:
F= (k q1 q2)/r2
where k=1/(4πε0) is the Coulomb constant = 8.988×109 m F-1.
The work done, U in moving the two protons together until they are attracted by the strong force is given by:
U=∫F.dr= (k q1 q2)/r0.
The limits on the integration are -∞ and r0.
The Coulomb barrier increases with increasing atomic number.
U=(k Z1 Z2 q2)/r0.
Where Z1 and Z2 are the proton numbers of the nuclei being fused. Using figures for 2 Deuterium nuclei, for which Z1,2=1, we obtain: U= (8.988 x 109 x 1 x 1 x (1.6 x 10-19)2)/(1 x 10-15) = 2.298 x 10-13 J
The kinetic energy of the nuclei is related to the temperature by:
(1/2) mv2 = (3/2) kBT
By equating the average thermal energy to the Coulomb barrier height and solving for T, gives a value for the temperature of around 1.1 x 1010 K.
In practice, this simple calculation overestimates the temperature. The temperature of critical ignition should be lower because there will be some nuclei with higher energies than average, however the temperature requirement is still to high for even these high energy nuclei. This treatment using classic physics does not take into consideration the effect of tunneling, which predicts there will be a small probability that the potential barrier will be overcome by nuclei 'leaking' through it.
Tunneling
Tunneling is a consequence of the Heisenberg Uncertainty Priciple which states that, the greater certainty we know the velocity of a particle the less we know about its position in space and vice versa
The uncertainty in the position is such, that when a proton collides with another proton, it may find itself on the other side of the Coulomb barrier and in the attractive potential well of the strong force. The probability of such an event happening decreases exponentially as the ratio of the classical turning point r0, to the de Broglie wavelength (&lambda=h/p).
P(tunneling) ∝ exp(-r0/λ)
We can now estimate the temperature for fusion to occur taking into account the tunnelling probability.
Rewritting the kinetic energy, in terms of the momentum p.
KE= (1/2) mv2 = p2 / (2m) = (h/λ)2 / (2m)
If we require that the nuclei must be closer than the de-Broglie wavelength for tunneling to take over and the nuclei to fuse.
Z1Z2q2/λ = (h/λ)2/(2m).
&lambda = (1/2) h2/(Z1Z2q2m)
If we use this wavelength as the distance of closest approach to calculate the temperature, we obtain
(3/2)kBT = Z1 Z2q2/(r)
The temperature is T = (4/3) (Z12Z22q4 m)/(h2kB).
For two protons this gives a temperature of 107 K.
Nuclear Fusion in the Stars
Before the process of nuclear fusion was known about, how the Sun and stars produced energy was a big problem in cosmology.
In 1848, J.R. Mayer examined the then-popular theory of the Sun being composed of burning coal. He stated that if the Sun began burning 5000 years ago, corresponding to the Biblical age of the Earth, then by his calculations, it already would have burned out.
The eminent physicist, Lord Kelvin, proposed several explanations on how the Sun might generate its energy including: mass contraction, which could allow the Sun to shine for up to 45 million years. At around the same time, Charles Darwin was looking at the erosion of rocks and concluded that the Earth had to be at least 300 million years old. The Sun had to be at least as old as the Earth so clearly the solution had not been found.
It was discovered that the when nuclei of hydrogen combine to form Helium, the resulting mass of was less than the sum of the mass entering the sum of the initial masses. The missing mass was converted into energy with an exchange rate of E=Δmc2 where Δm is the difference in the mass of the nuclear reaction and c is the speed of light (3 x 108 m s-1). The conversion of a relatively small amount of mass into energy would allow the Sun to shine for billions of years.
The fusion of Hydrogen into Helium in stars occurs in three stages. First, two ordinary Hydrogen (Hydrogen-1) nuclei, which are actually just single protons, fuse to form an isotope of Hydrogen called Deuterium (Hydrogen-2), which contains one proton and one neutron. A positron (a positively charged electron) and a neutrino (a neutral particle which travels nearly at the speed of light and has, perhaps, almost no mass) are also produced. The positron is very quickly annihilated in the collision with an electron and the neutrino travels right out of the Sun.
11H +11H = 21H+ 00e+ +00ν
The newly-formed Deuterium fuses with another regular Hydrogen to form an isotope of Helium, Helium-3 containing two protons and one neutron.
21H+ 11H = 31H
Next, two of the Helium-3 nuclei fuse to form a Helium-4 nucleus and two hydrogen-1 nuclei. Energy as gamma rays are produced in each step.
31H+31H = 42He + 210H
The resulting reaction cycle generates around 25 MeV of energy. Another series of reactions may occur in stars hotter than the Sun. such as the Carbon-Nitrogen cycle, in which a Carbon nucleus is involved in the first step. Here again, the overall result is to combine four Hydrogen nuclei to form one Helium nucleus. Other cycles, involving Nitrogen and Oxygen, have been proposed for explaining the fusion process in even hotter stars. The high density of the Sun allow the temperature for fusion to occur to be around 1.5 x 107 K
Nuclear Fusion on Earth
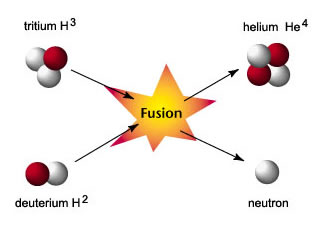
Man-made nuclear fusion uses a different reaction to that which occurs in the stars. In stellar Hydrogen burning, the reaction of two Helium-1 nuclei requires a proton to change into a neutron. Fusion on Earth starts by fusing Deuterium and Tritium. (Tritium is an isotope of Hydrogren which contains 1 proton and 2 neutrons.) The reaction proceeds as follows:
21H + 31H = 42He + 10n + 17.59 MeV.
An equally probable reaction can also occur between two Deuterium nuclei in one of two ways:
21H +21H = 32H + 10n + 3.27 MeV
or alternatively,
21H +21H = 31H + 4.03 MeV
Conditions for Break-Even
The heating of the plasma requires an enormous amount of energy and for the plasma to be self-sustaining it must produce at least the same amount of energy that it uses. There are three parameters that must be considered to 'break-even'.
- The plasma temperature - the temperature for fusion to occur depends on the kinetic energy required by the nuclei to overcome the repulsive Coulomb barrier at a distance of 10-15 m.
- The plasma density - once the temperature is high enough to initiate fusion, the ion density must be high enough to ensure that the collisions release more energy than they need to start.
- The confinement time - the confinement time is defined as the time the plasma spends above the critical ignition temperature
Each of these factors is bundled into a performance figure known as the Lawson criteria. Its sets the lower bound on break-even. That is to say, if your plasma has a lower figure than the Lawson criteria you are using more energy than you are producing. Current fusion reactors use up more energy than they put in.
- D-T fusion n τ ≥ 1014 cm-3 s-1
- D-D fusion n τ ≥ 1016 cm-3 s-1
Nuclear Fusion Reactors
The earliest patent for a nuclear fusion reaction was made in 1949. Since that time many designs have been tried. One of the problems is to contain the plasma. In stars, the huge mass of the star is enough to allow gravity to confine the plasma. This option is not available on Earth, however, since the plasma is a mixture of positively and negatively charged particles, it can manipulated by a magnetic fields.
The Magnetic Mirror
In the sixties and seventies, machines using magnetic mirror confinement were considered a viable candidate for producing fusion energy. Collisions scattered the charged particles so that the pitch angle was too small for containment. In addition, velocity space instabilities contributed to the escape of the plasma.
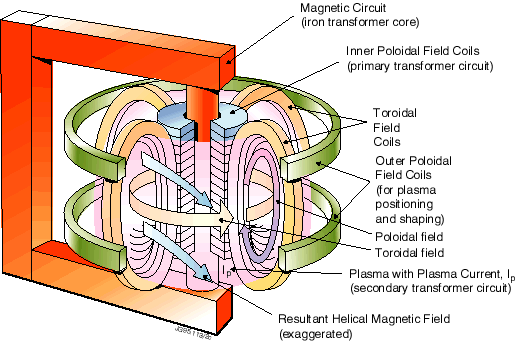
The Tokamak
The tokamak uses magnetic fields to confine a plasma to the interior of a torus shaped vacuum chamber. When the plasma has been heated to around 100 million K fusion occurs. Each fusion reaction results in the production of an alpha particle (42He nucleus) and a neutron. The neutrons carry most of the energy and can escape the confining fields. They are captured in the walls of the tokamak where they generate heat. A coolant circulating through the walls is passed through a heat exchanger to produce the steam to drive turbines, as in a conventional power station. The walls also double as a "breeding blanket" in which neutrons react with Lithium to produce further Tritium.
using magnetic fields
Plasma Confinement
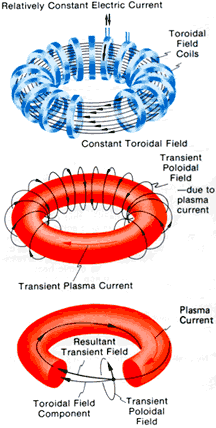
Confinement of the plasma is achieved by two superimposed magnetic fields which enclose the plasma: the toroidal field generated by external coils on the one hand and the magnetic field due to the flow of the plasma. In the combined field, the field lines run helicoidally around the torus centre. In this way, the necessary twisting of the field lines and the structure of the magnetic areas are achieved. In addition to the toroidal field generated by the external field coils and the field generated by the flow in the plasma, the Tokamak requires a third vertical field (poloidal field), which acts to position the flow in the plasma container. The plasma current is normally induced by a transformer coil.
Plasma Heating
Heating the plasma can be achieved using one or a combination of the following methods:
- Ohmic Heating - since the plasma is a conductor, it can be heated by passing a current through it. The tokamak works like a giant transformer, the primary windings are physical coils, the secondary coil is the plasma. The heat generated depends on the resistance of the plasma and the current. But as the temperature of heated plasma rises, the resistance decreases and the ohmic heating becomes less effective. It appears that the maximum plasma temperature attainable by ohmic heating in a tokamak is 20-30 million degrees Celsius. To obtain still higher temperatures, additional heating methods must be used.
- Neutral-Beam Injection - involves the introduction of high-energy (neutral) atoms into the ohmically heated, magnetically confined plasma. The atoms are immediately ionized and are trapped by the magnetic field. The high-energy ions then transfer part of their energy to the plasma particles in repeated collisions, thus increasing the plasma temperature.
- Radio Frequency (RF) Heating - high-frequency waves are generated by oscillators outside the torus. If the waves have a particular frequency (or wavelength), their energy can be transferred to the charged particles in the plasma, which in turn collide with other plasma particles, thus increasing the temperature of the bulk plasma.
Stellarators
One of the problems with tokamak devices, is the windings confining the plasma within the torus are less dense on the outside of the loop than on the inside. Therefore, the plasma on the inner portion of the tube would thus see a greater magnetic force than those at the outside, and only particles near the middle would experience the correct force to keep them confined. Since the magnetic forces is at right angles to motion, a non-centered plasma moving around the toroid would thus be forced up or down until it hit the inner wall of the torus.
The earliest stellarators were literally figure-eights, consisting of two sides of a torus connected together with crossed straight tubes. This arrangement was less than perfect. Various different geometries were tried to address the problems. Later version reduced the problem by introducing a "peanut" shaped tube instead of a figure-of-eight. The in-bent sides offsetting the out-bend toroidal sections on either end.
But the real solution turned out to be magnetic instead of mechanical: by rotating the magnetic windings themselves as they were wrapped around the chamber, the plasma would be rotated around a simple torus, slowly moving from inside to outside as shown in Figure 5.

Inertial Confinement
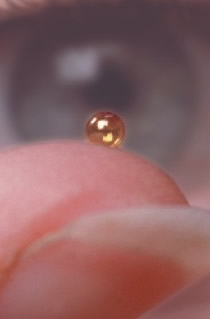
micro-balloon fuel pellet.
In a Tokamak, the confinement time is long compared with the density. Inertial confinement creates a very dense plasma for a short length of time. Inertial confinement fusion works by compressing a small mirco-balloon filled with a low density mixture of Deuterium and Tritium (Figure 4.). Compression is facilitated by targeting the micro-balloon with high-powered laser beams from all sides. As shown in Figure 5.

fusion reactor in action.
Figure 6. shows the stages of inertial confinement fusion process. When the laser-beams are fired, they focus an enormous quantity of energy onto the shell of the micro-balloon, vaporising it almost instantly producing a surrounding plasma envelope. The fuel is compressed by the blow-off of the hot surface material which creates a shock-wave that compresses an heats the fuel. During the final part of the implosion, the fuel core reaches 20 times the density of lead and ignites at 100 million K. This temperature is high enough to ignite the fusion reaction.
Heating the micro-balloons with lasers focused on to the target is known as direct drive. A second method to initiate fusion, know as indirect drive, uses a cylindrical hollow cavity, called a hohlraum, in which the micro-ballon is placed. The lasers striking the metalic surface are converted into x-rays. The x-rays heat the microballon in more symmetric way leading to a more uniform implosion.
Cold Fusion
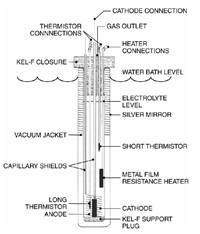
In 1989, an experiment performed at the University of Utah by Pons and Fleischmann's which claimed to have demonstrated fusion. The experiment was essentially an electrolysis cell, consisting of Platinum and Palladium electrodes placed in heavy-water (D2O). When the experiment was performed, it was found that the more heat was produced than can could be accounted for by chemical processes alone. Pons and Fleischmann concluded that the excess heating must be nuclear in origin.
The experiment hinges on the accuracy of the calorimetry used to determine the heating. More accurate calorimeters were tried and the heating effect was found to be significant. Other researchers found it difficult to reproduce the results so, after an initial media frenzy, the claims were widely dismissed.
Despite the general lack of acceptance by the mainstream scientific community, research continues by a few. In 2004, the Department of Energy peer reviewed the experimental evidence for cold fusion. It concluded that:
The experimental data shows evidence of: the existence of a physical effect that produces heat in metal deuterides.
The production of 42He in amounts commensurate with a 21H + 21H -> 42He reaction mechanism, a physical effect that results in the emission of energetic particles
The underlying process that produce these results are not manifestly evident from experiment. The scientific questions posed by these experiments are both worthy and capable of resolution by a dedicated program of scientific research.
Bubble Fusion
Sonoluminesence is the production of light from sound. It was first obversed in 1934, yet comparatively little is known about the process. Ultrasound in water can lead to the expansion and contraction of small bubbles dissolved in the water. In the reifaction, the bubble expands while during the compression, the bubbles collapse rapidly (1.4 km s-1 at the point of light emission) leading to a compression of the gas inside. The compression halts when the van der Vaals forces between molecules will not allow them to get any closer. The mechanism for the light emission is proposed by the shock-wave model.
The shock-wave model of sonoluminescence has the collapsing bubble generate an imploding shock-wave which focuses at a point. As the shock-wave propagates, it heats and intensifies the gas it passes through. At the focus, the shock-wave bounces back and makes the gas even hotter. Light is emitted because the shock-wave heats the gas enough to become ionised. The electrons emit light when they collide with the ions which results in the observed continuous emission spectra.
Experiments measuring the emission wavelength, show it to correspond to an energy of around 6 eV, which in turn, corresponds to a temperature inside a collapsing bubble of 70,000 K. There may be photons of even higher energy which would mean higher temperatures, but these wavelengths are absorbed by the water so it is not known what the maximum temperature inside the collapsing bubble is. It is at this point we turn our attention to fusion.
While 70,000 K is far below the 100 million K required for fusion, the temperature of the gas in the centre depends on the minimum size of the of the collapsing bubble. This is another unknown. The so-called shock radius, the radius of the bubble at the point of sonoluminescence, is around 0.1 μm but its minimum size could be smaller for an emission energy of 6 eV. If the radius of the bubble reaches 10 nm (just 10 times smaller) and the gas inside where deuterium, fusion could be ignited. Experiments producing sonoluminescence in deuterated acetone have claimed to produce nuclear fusion with the tell-tale emission of neutrons. Once again, the reproducibility of these results is at issue since it is very difficult to tell whether the neutrons were produced by nuclear processes or part of the background neutron count.
