The Chinese discovered the magnetic compass as early as 200 BC. The ancient Greeks knew that the lodestone or magnetite attracted iron towards it. It is known that the Vikings used a lodestone to navigate. Later at the end of the twelfth century Europeans were using this simple compass to aid navigation. A steel needle stroked with such a "lodestone" became "magnetic" as well.
In 1600, William Gilbert of Colchester, physician to Queen Elizabeth I, proposed an explanation, in his work De Magnet for the operation of the compass. The Earth itself was a giant magnet, with its magnetic poles some distance away from its geographic ones (i.e. near the points defining the axis around which the Earth turns).
A magnetic field are the lines of force generated by a magnetic. By convention the arrow tip on magnetic field lines points towards the south magnetic pole and away from the north magnetic pole. The magnetic poles alway occur in pairs, no one has ever found a magnetic monopole, though there is research into their posible existance. If a bar magnet is broken in two, at the fracture new north and south poles are formed at the point of fracture.
| Source | Magnitude of B (T) |
|---|---|
| A hair dryer | ~10 -7-10-3 |
| Sunlight | ~ 3 x 10-6 |
| Colour TV | ~ 10-6 |
| A small bar magnet will produce | ~10-2 |
| At a sunspot B | ~ 0.3 |
| MRI body scanner magnet | ~ 2 |
| Reseach Physics Labs produce up to | ~50 |
| The field at the surface of a neutron star | ~108 |
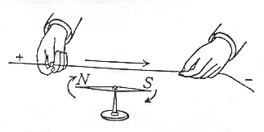
Electricity and Magnetism are not seperate phenomena, they are closely linked. When a current flows through a conductor it generates a magnetic field around the conductor. This was discovered by Han Christian Ørsted in 1820 when he noticed after giving a lecture that a current flowing though a wire deflected a compass needle, placed parallel to the wire.

It takes quite a large current to produce a measurable effect which may account for it not being discovered before.
The current causes a magnetic field lines around the diameter of the wire.
The flux density in a magnetic field is given the by the force F/Il where F is the force on the wire, I is the current flowing through the wire and l is the length of the wire in the field.
The flux density or B field is defined as the force on a wire at right angles to the magnetic field per unit length per unit current. B=F/IL.
For a particle, with a velocity perpendicular to the magnetic-field, the force is perpendicular to the velocity this causes the charged particle to move in a circular path. The acceleration providing the centripetal force is given by a= v2r. The magnitude of the acceleration on the particle is given by a=qBv/m. Equating the two. mv2/r=qBv/m.
Therefore the radius, is given by r= mv/qB. This is known as the Lamour radius
The distance travelled by the particle, if it rotates in a circle of radius r is 2πr. If it travels at a velocity, v then the time,T to complete a single revolution is v/(2&pi r)=2πqB/m.
The inverse of this, or fc=m/2πqB gives the Cylcotron frequency.
The cyclotron is a device that accelerates particles using a high-frequency electric field. Physically, it consists of two, D-shaped metallic boxes known as dees in a magnetic field. A charged particle is injected into the dees and the electric field accelerates the particle, while the magnetic field constrains the particle in a circular path. As the particle is accelerated by the electric field, the radius of the particles path increases, and the particle spirals outward.
The unit of charge is the Coulumb, [C], but the SI unit is the [As-1] the Ampere. Why is this? Quite simply it is because it we can measure the current more accurately than the charge. And the Ampere is defined in terms of the magnetic field produced by a current flowing in two parallel wires. To be more specific, the definition is
The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 metre apart in vacuum, would produce between these conductors a force equal to 2 x 10- 7 Nm-1 of length.
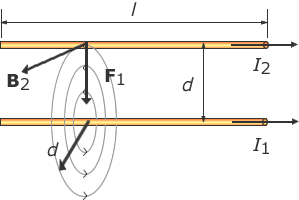
The magnitude of the force of wire 1 on wire 2, is given by F1=B1I1l from the Biot-Savart Law, the magnetic field is given by B=μ0I1I2/(2πd). Rewritting the force as the force per unit length is then F1/l=μ0I1I2/(2πd). With I1 and I2= 1, d=1 m the force per unit length is 2 x 10-7 Nm-1 giving the definition of the Ampere.
Ampere's Law states that the distance around lines of magnetic field B.ds around any closed path equals μ0 times the current, I is the total steady current intercepted by the surface bounded by closed path.
Mathematically, ∮B.ds=&mu0I
The Biot-Savart Law is the magnetic equivalent of Coloumbs Law for electric fields. It allows us to relate magnetic fields to the currents which are their sources. Where as Coulombs law relates electric field to the point charges which are their sources. The Biot Savart law is expressed as a differential and the resulting magnetic field is solved using calculus often simplified by the symmetry of the particular problem.
The Biot Savart Law is given by
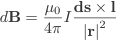
The results for calculating the magnitude of the magnetic field, B obtained by applying the Biot-Savart law for various geometries are shown below. The derivations can be found separately on this page
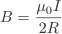
Where R is the raidus of the loop in metres.
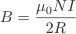
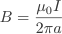
In this instance a is the distance from the wire.
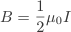
It is one of the oldest puzzles in physics is the asymmetry between electric and magnet fields. An electric field can be formed by a single positive or negative charge. However, magnetic fields can only be formed by a dipole. Why can't a magnetic field by produced by a single magnetic pole? The theory of magnetic monopoles was originally proposed by Paul Dirac. However, so far all experimental searches for the existance of magnetic monopole has come to nought. No one has ever observed a magnetic monopole. However, if magnetic monopoles were discovered it would account for the quantisation of charge.