Potential V is defined as the potential energy per unit charge.
V = E/q
It is a scalar
Electric potential is often called the voltage, because the unit of potential is the Volt.
Electrical potential energy can be measured by considering the electrical energy of a point charge in an electric field of another point charge q0.
We know that when a charge is a in an electric field their is a force acting on it. The energy or work required to move the charge in this electrical field is given by
where dl is a small (infinitesimally small) distance moved by the charge.
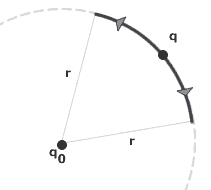
We can see that when the test charge moves in an circular arc centered around the point charge q the radial distance of the test charge from the charge producing the electrical field does not change and so the electrical potential energy is 0.
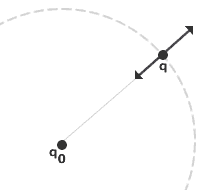
If the test charge moves away from q0 so its radial distance changes there will be a change in potential energy. Suppose it moves from point a to point b. The change in potential energy will be
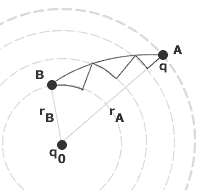
Suppose that the test charge moves along an arbitrary path. However the charge moves, its motion can be thought of as being composed of an infinite number of circular and radial paths. When you add all the terms, the only terms that don't cancel each other out are the starting point and the end point, because for all the small radial movements one end point from one radial jump is the start point of the next.
The final result is that only the distances of the initial point A and final point B count to change the potential energy.
So the change in electrical potential energy is
Even though the motion was in two dimensions it can be seen that it is still valid for motion in three dimensions. Only the motion along radial distances counts in the change of potential energy.
To find the electrical potential energy of our test particle in an electric field composed of a number of point charges, we can use the principle of superposition which allows us to sum the potential energies found by considering each individually.
i.e.
Since only differences in potential energy make physical sense, it is convenient to choose some point where the potential is zero. For the charges in this example the zero of potential would be out at infinity, however it depends on the type of problem.
We can see that eletrical potential energy is analoguous to gravitational potential energy only in this case we take the zero of potential to be at the surface of the Earth, hence. P.E. = m g h, where h is of course the height above the Earth's surface.
Now we can arrive at an expression for potential. Potential is defined as